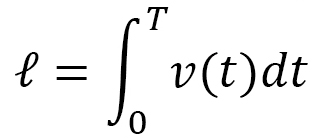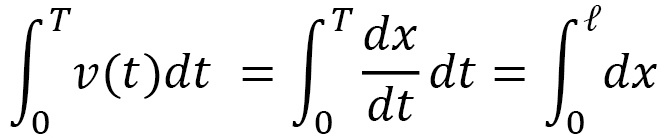研究概要
Finsler 幾何とは?
A.物体の運動と最短距離
物体の運動は、力が働いていない場合には直線運動します(図1)。この直線運動においては、物体が進む距離 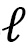 は、その速さ
は、その速さ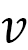 と時間
と時間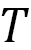 によって決まり,距離は速度×時間となります。速度が変化するような一般の場合も含めて考えると,
によって決まり,距離は速度×時間となります。速度が変化するような一般の場合も含めて考えると,
のように,積分で表わされます。さらに、この距離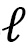 は、速さ
は、速さ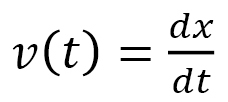 を使えば
を使えば
のように、実数上の積分で表わせます。この式を、距離を求める公式と見れば、速さという物体の運動の個性がなくなっているように見えます。
このことから、この距離 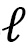 が平面上の2点P,Q間の距離だとすると、
が平面上の2点P,Q間の距離だとすると、
- 物体は力が働かない場合はその速度によらず直線運動する
- その直線距離
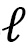 は2点間の最短距離になる
は2点間の最短距離になる
(A-1)
と表わすことができます。
しかし、この法則(A-1)はどんな場合でも正しいでしょうか?
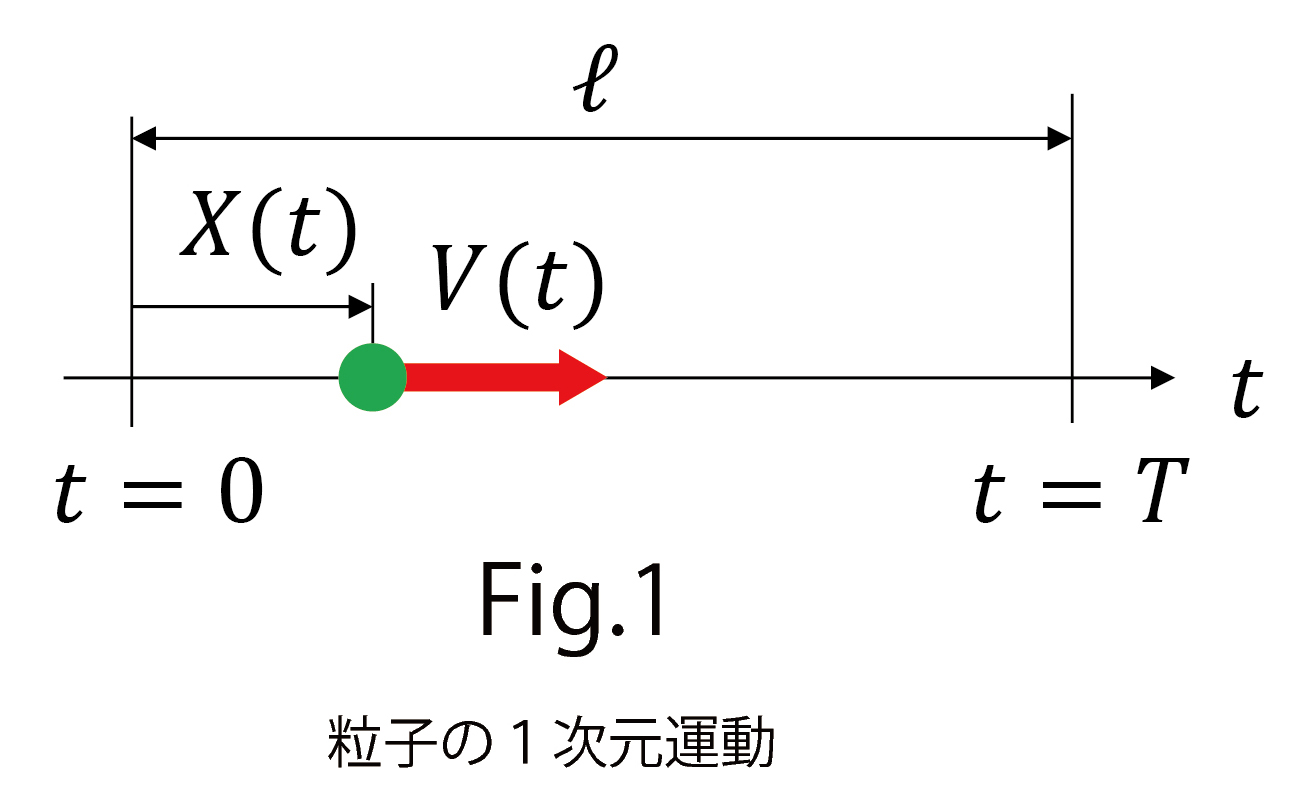
例えば、物体が光だとして、その光が水の中から空中に進むときを考えてみましょう(図2)。図2のように光は、屈折という現象で知られていますが、点Pから点Qまで直線的には進みません。その理由としては、水中での光の速度が空中よりも遅くなるためであることがわかっています。実際は、光は、2点PQ間を「最短の時間」で進むことから,このように屈折することが分かっています。
この光の屈折現象が上記の法則(A-1)で説明できない理由は,「速度という運動の個性」を無視したためであると考えることもできそうです。
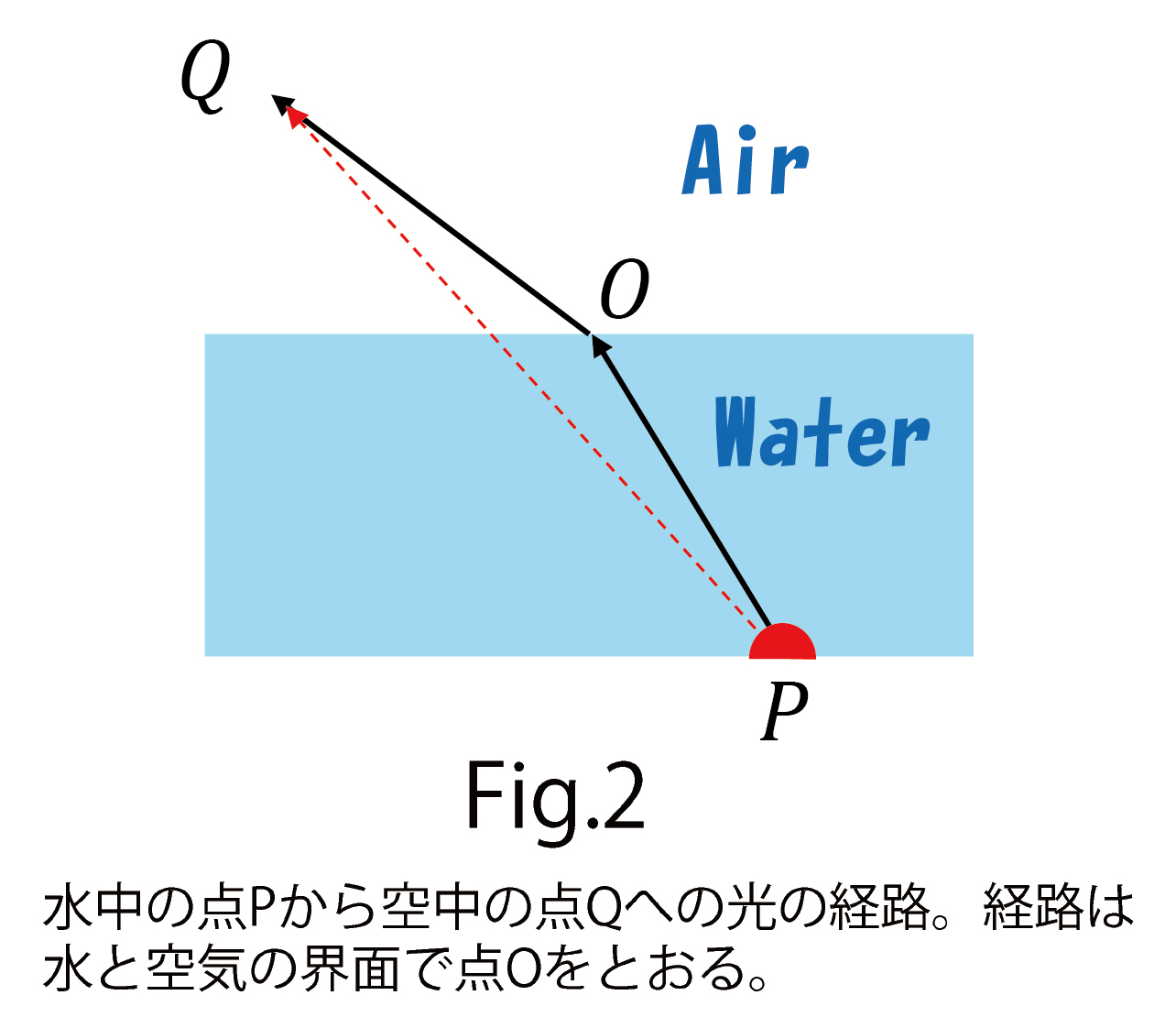
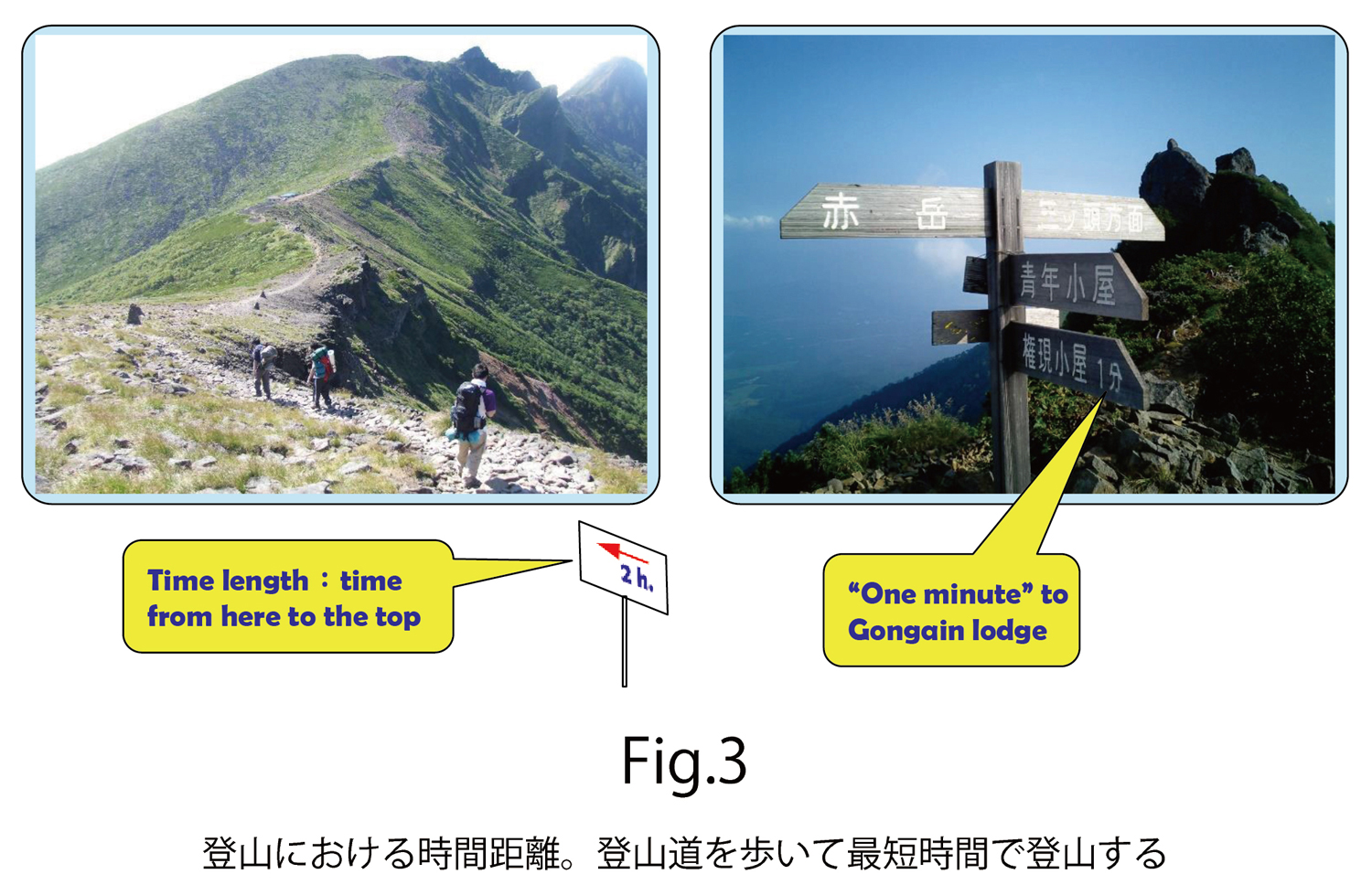
もう一つの例として、山登りを考えましょう(図3)。この場合、登山者が物体で、その歩く速さが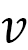 です。登山道は、例えば、ふもとから頂上までの経路を考えると、その経路は最短距離ではありません。むしろ、ふもとと頂上を最短時間で結ぶ経路といえます。図3の写真にもあるように、多くの場合、山の峰を通るような曲がりくねったものです。
です。登山道は、例えば、ふもとから頂上までの経路を考えると、その経路は最短距離ではありません。むしろ、ふもとと頂上を最短時間で結ぶ経路といえます。図3の写真にもあるように、多くの場合、山の峰を通るような曲がりくねったものです。
山では,写真にもありますが,ここから山頂まで「2時間」というように,距離は時間で表示されています。頂上の山小屋まで行くのにどのくらいの時間がかるか,または,頂上まで行って戻るのにどのくらいの時間がかかるか,が一番の問題だからです。山登りは「時間距離」に支配されているのです。
さらに,山登りでは,登りは「2時間」下りは「1時間」のように、行きと帰りの時間距離が違います。これも,登山者が山を登るときに歩く速さと,下りでの歩く速さが違うためです。
このように,速さの違いからくる「時間距離」という普通と違う距離を用いることで,法則(A-1)が,光の屈折現象や山登りに対しても,それほど修正なしに成り立ちそうです。ただし,この時間距離をきちんと定式化するには「時間距離」を数学的に定義する必要があります。これは,Finslerによってなされました(文献[1])。
B.物体の運動にかかわる時間距離
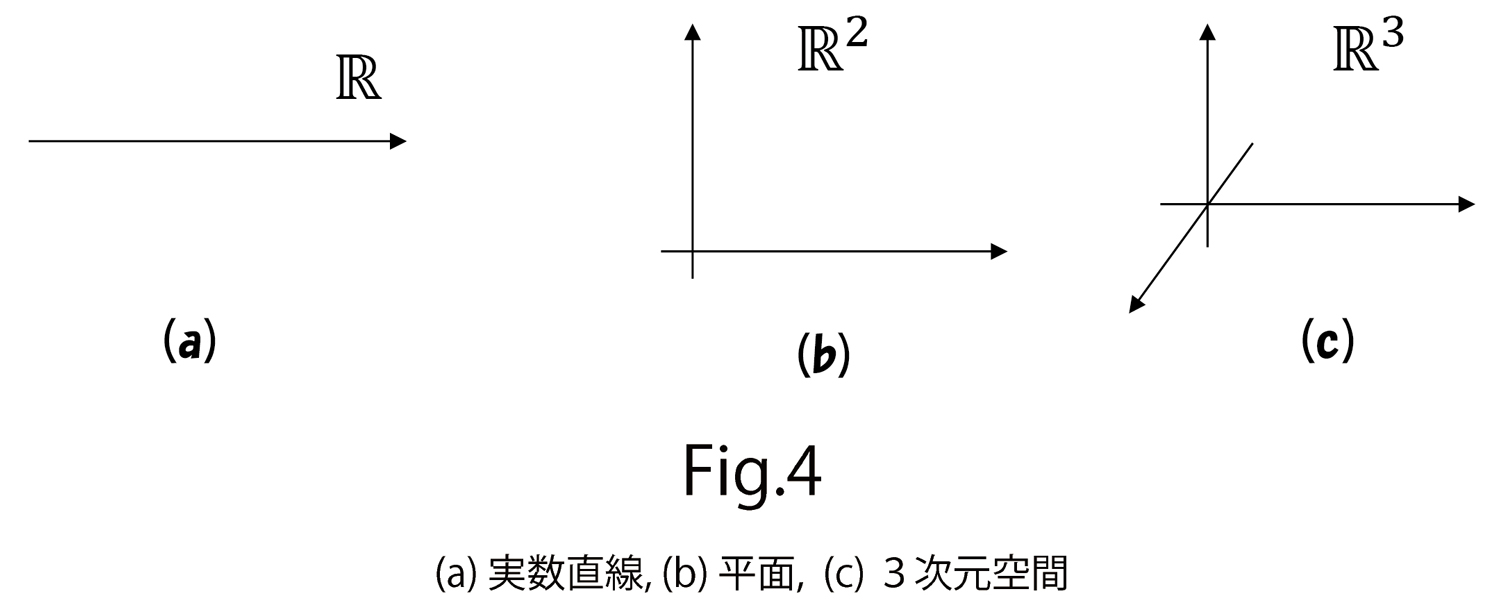
Finslerによって導入された時間距離に進む前に、普通の距離について考えてみましょう。物理の問題を解くときには数の計算で行いますから、位置や速度もその数で表わしますので、数学的には「実数の距離」といえると思います。実数直線を2本垂直に書けば平面になり、3本で普通の3次元空間になります(図4)。物理では、先にも出ましたが、真空中を光が進む速さ(速度ベクトル)を1として、距離を定義します。物理では単位があり、細かく指定しないといけないですが、単位を定めて距離が1[m]となったとき、この1[m]を実数直線上の1とすれば、結局、物体の運動は実数直線上で考えればいいということになります。
- 文献[1]:松本誠、計量微分幾何学、裳華房、1975年
では、Finslerが導入した「時間距離」はどのようなものでしょうか?
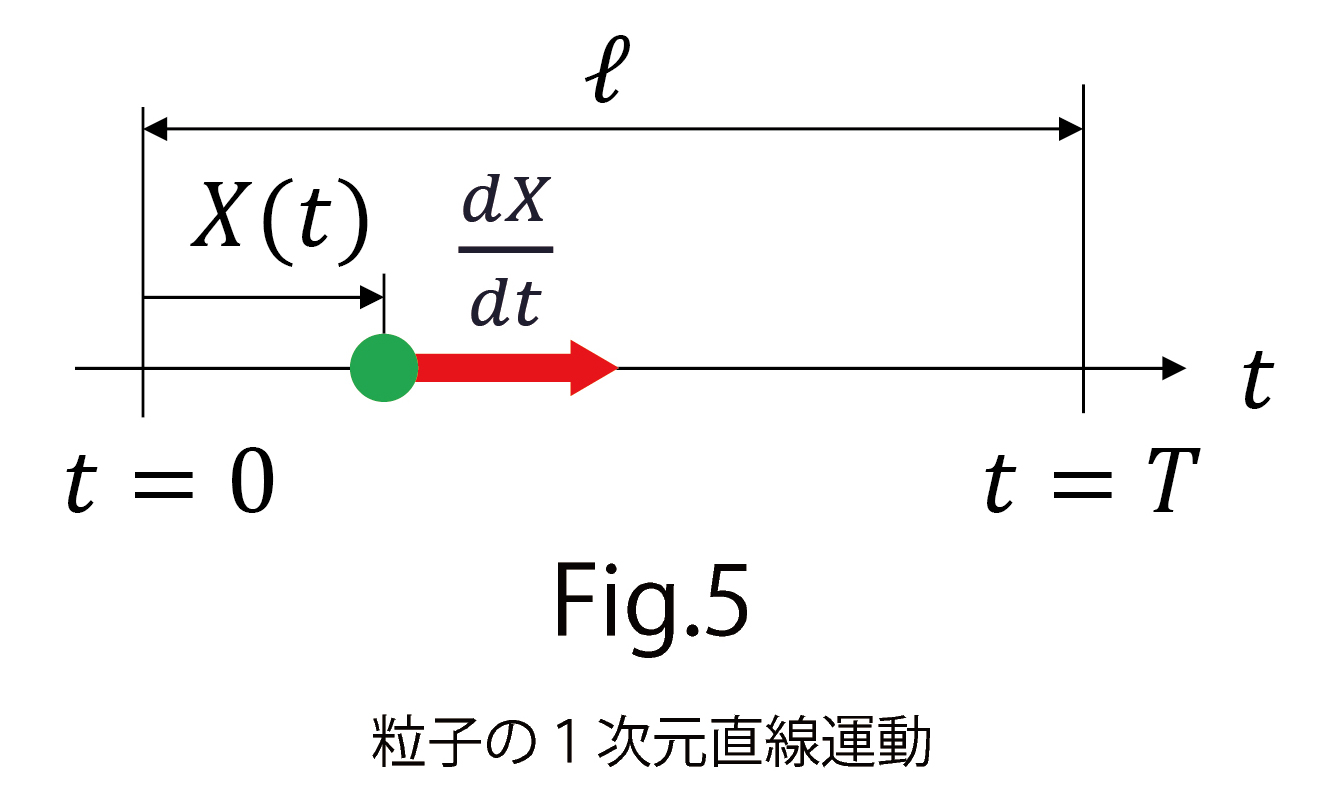
ここでは、文献[1]に書かれている内容を物体の直線運動に限定して、筆者の理解の範囲内で説明いたします。物体の位置を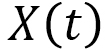 、速度を
、速度を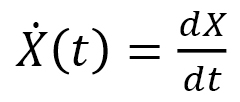 とし、
とし、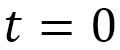 から
から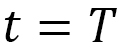 間に距離
間に距離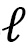 だけ進むとします(図5)。さらに、速度
だけ進むとします(図5)。さらに、速度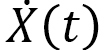 と同じ方向に、
と同じ方向に、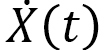 と同じは限らない別な速度
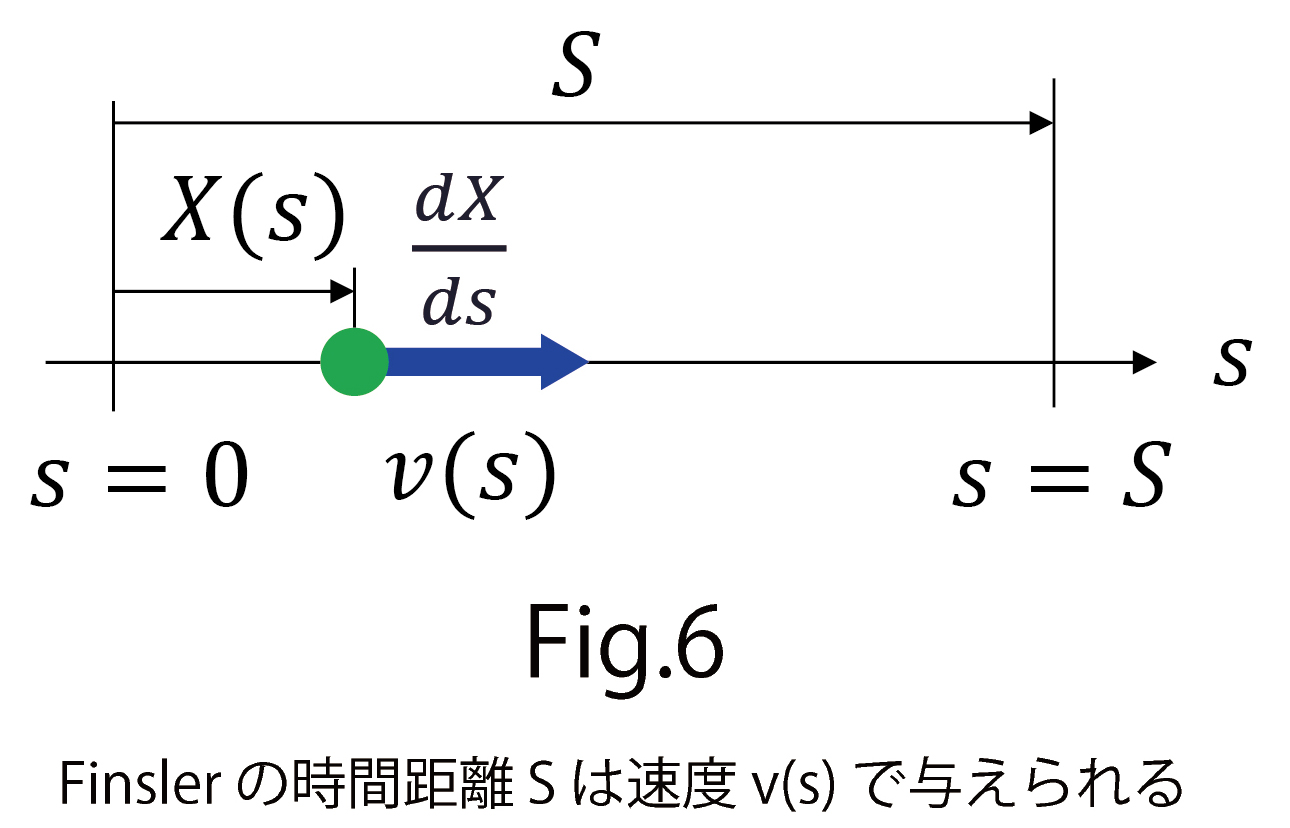
と同じは限らない別な速度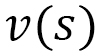 で動く場合を考えます (図6) 。このとき、時間
で動く場合を考えます (図6) 。このとき、時間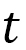 の代わりに、パラメータ
の代わりに、パラメータ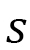 を
を
(B-1)
となるように定義します。このパラメータ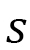 と時間は、時間の単位の変換のように、互いに一方が他方の関数になっているとします。このパラメータ
と時間は、時間の単位の変換のように、互いに一方が他方の関数になっているとします。このパラメータ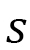 はその
はその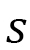 に関する速度
に関する速度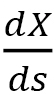 が、与えられている
が、与えられている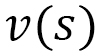 と等しくなるように定義されたパラメータで、Finslerの「時間距離」といわれるものです。またこの
と等しくなるように定義されたパラメータで、Finslerの「時間距離」といわれるものです。またこの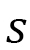 はFinsler関数と呼ばれる位置と速度の関数
はFinsler関数と呼ばれる位置と速度の関数
(B-2)
から
(B-3)
によって求められます。実際、
(B-4)
となります。(B-4)を時間距離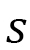 の定義とすることもできます。この
の定義とすることもできます。この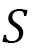 は積分変数を取り換えても値は変わりません。このことから、
は積分変数を取り換えても値は変わりません。このことから、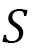 は直線上の普通の距離
は直線上の普通の距離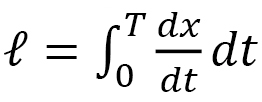 (図5)とは異なった距離になることがわかります。
(図5)とは異なった距離になることがわかります。
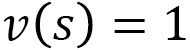 なら
なら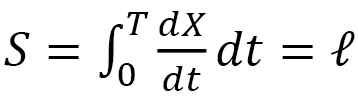 となって、
となって、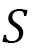 は普通の距離になります。また、
は普通の距離になります。また、 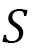 は、
は、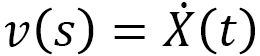 のとき、すなわち
のとき、すなわち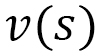 が物体の速度に等しいときには、
が物体の速度に等しいときには、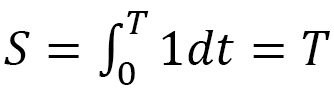 となり、時間になることから、時間距離と呼ぶことができます。
となり、時間になることから、時間距離と呼ぶことができます。
この時間距離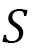 の特徴は、向きに依存することです。このことは
の特徴は、向きに依存することです。このことは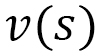 が向きによって異なってよいからです。図6で距離
が向きによって異なってよいからです。図6で距離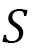 を
を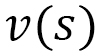 の向きと同じ向きの矢印で書いているのはこのためです。逆向きにはまた別の
の向きと同じ向きの矢印で書いているのはこのためです。逆向きにはまた別の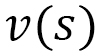 から決まる別の
から決まる別の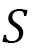 になります。これは普通の距離(図5)には無い性質で、これが次に述べる材料の異方的変形への応用につながります。
になります。これは普通の距離(図5)には無い性質で、これが次に述べる材料の異方的変形への応用につながります。
C.時間距離の材料科学への応用
ここでは、Finslerの時間距離の持つ特徴、距離の方向依存性(行きと帰りで時間距離が異なる)を生かして、材料科学への応用:材料の異方的変形、を考えます(文献[2])
C-1.液晶エラストマの電場による異方的変形(文献[3,4])
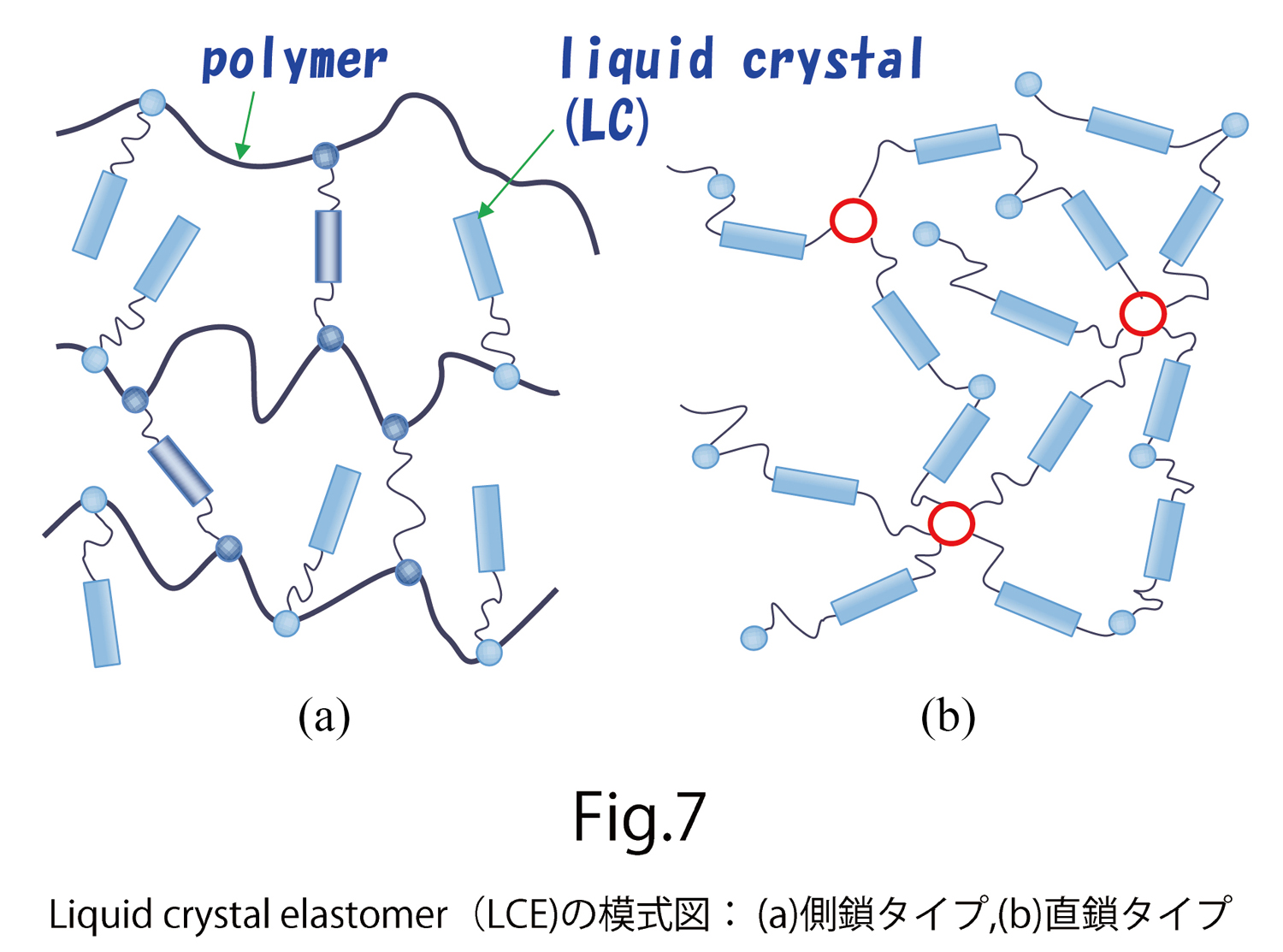
材料の異方的変形の典型例として、液晶エラストマーと呼ばれる、液晶分子とゴム分子(ポリマー)が化学的に結合した物質を考えます(図7)。液晶エラストマーは、電場をかけると図のように電場方向に延びてそれと垂直方向には縮みます(図8) 。
問題はなぜこのような変形が起こるのかということです。この問題は、各分子間の厳密な相互作用を考慮したいわゆる第一原理計算など、すでに多くのアプローチによって解かれていますので、ここに示す方法はその中の一つにすぎません。
ポリマーだけに着目するとその張力エネルギー(ハミルトニアン)は、
(C-1)
のようにモノマー間の距離の2乗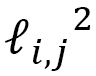 の和によって表わされます。ここで、
の和によって表わされます。ここで、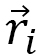 はi番目のモノマーの位置ベクトル、
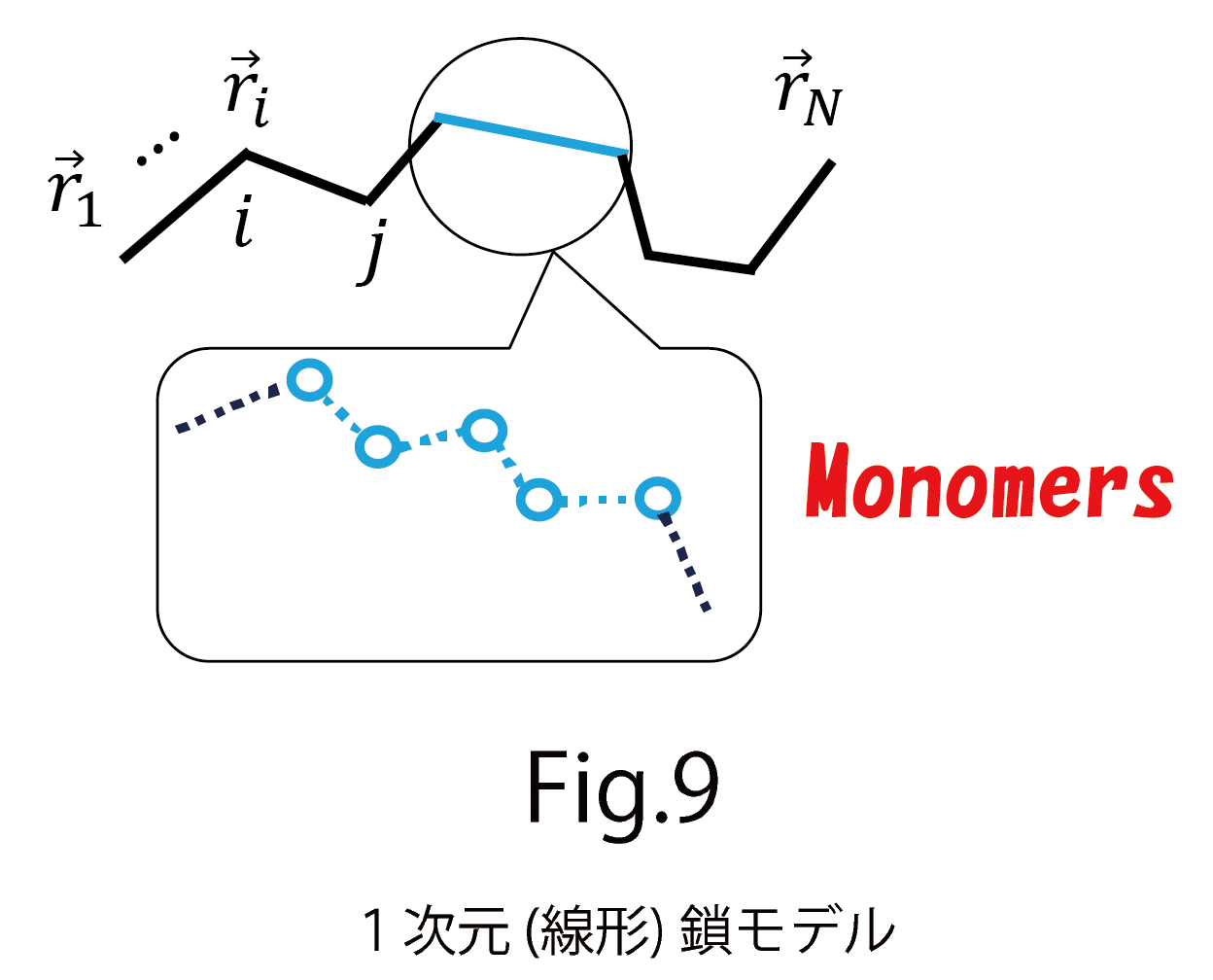
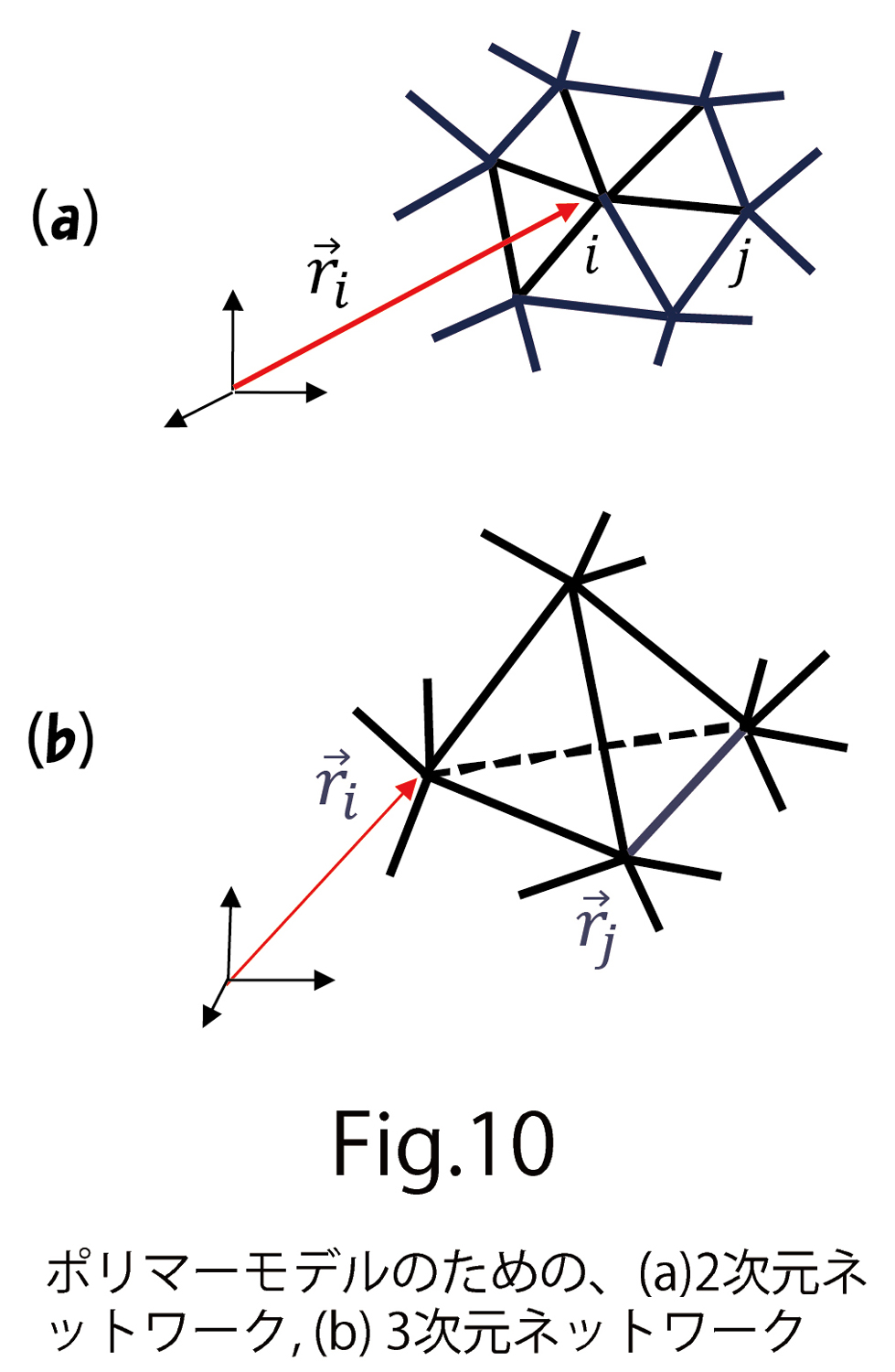
はi番目のモノマーの位置ベクトル、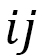 は隣り合う2つのモノマーの番号を指しています(図9) 。このようなハミルトニアンを仮定するモデルは、1次元の場合は「線形鎖モデル」と呼ばれて、ポリマーの分野では有名なモデルです。ここでは、その1次元鎖を2次元のネットワーク、さらに3次元のネットワークに拡張したものを考えます(図10)
は隣り合う2つのモノマーの番号を指しています(図9) 。このようなハミルトニアンを仮定するモデルは、1次元の場合は「線形鎖モデル」と呼ばれて、ポリマーの分野では有名なモデルです。ここでは、その1次元鎖を2次元のネットワーク、さらに3次元のネットワークに拡張したものを考えます(図10)
式(C-1)のは積分で書けば
(C-2)
のように、局所座標系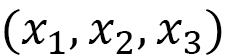 の3次元積分で表わされます。
の3次元積分で表わされます。
式(C-1)のハミルトニアンは、ある方向にだけ変形しやすいような性質は持っていません。従って、等方的なハミルトニアンといえます。変形の異方性を考慮するには、液晶分子からくる異方性をこのハミルトニアンに加える必要があります。
- 文献[2]:H.Koibuchi, H. Sekino, Physica A 393, pp.37-50 (2014) https://doi.org/10.1016/j.physa.2013.08.006
- 文献[3]:E.Proutorov, H.Koibuchi, J. Phys. (Cond.mat.)30,405101(2018) https://doi.org/10.1088/1361-648X/aadcba
- 文献[4]:K. Osari, H.Koibuchi, Polymer,114,pp.355-369(2017) https://doi.org/10.1016/j.polymer.2017.02.065
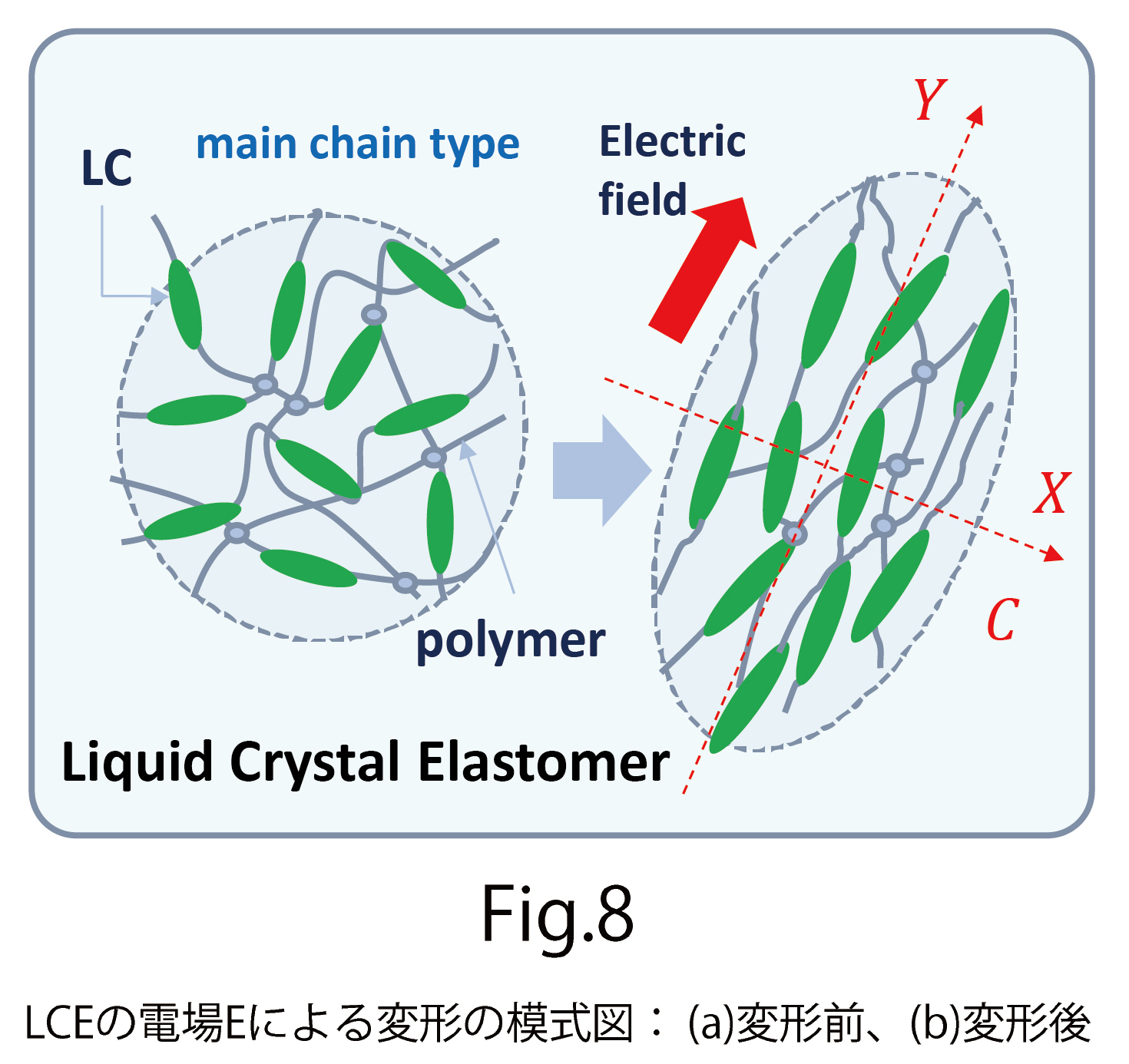
この目的のために、3次元の弾性エネルギーを、図8の点線X軸に沿った1次元直線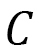 に制限したもの
に制限したもの
(C-3)
を考えます。簡単のため、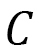 軸は外側の座標系のX軸に平行としています。直線
軸は外側の座標系のX軸に平行としています。直線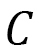 上の局所座標系を
上の局所座標系を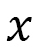 とすると、和
とすると、和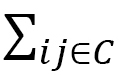 は
は
(C-4)
となります。従って、導関数は
(C-5)
となります。
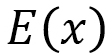 を導入する理由は、物体の運動の場合と違って、各分子はその位置が移動するわけではないからです。そこで、物体の位置
を導入する理由は、物体の運動の場合と違って、各分子はその位置が移動するわけではないからです。そこで、物体の位置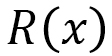 の代わりに、C軸上の状態関数として
の代わりに、C軸上の状態関数として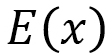 を考えます。この
を考えます。この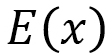 はC軸に沿った1次元的な弾性エネルギー(の1次元積分)として定義していますので、物体の位置
はC軸に沿った1次元的な弾性エネルギー(の1次元積分)として定義していますので、物体の位置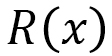 と同じように、
と同じように、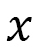 とともに増えます。1次元の物体の運動との対応は
とともに増えます。1次元の物体の運動との対応は
| 現象 | 座標関数 | 異方性の原因 | Finsler 距離の定義式 | 異方的性質 |
|---|---|---|---|---|
| 物体の運動 | 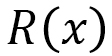 |
方向依存の速さ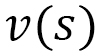 |
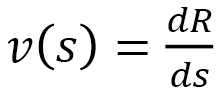 |
sの方向依存性 |
| 液晶エラストマ | 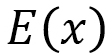 |
内部状態の向き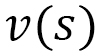 |
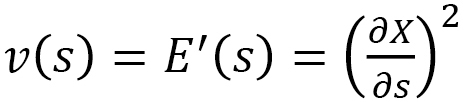 |
sの方向依存性 |
のようになります。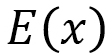 はFinslerの時間距離を決めるので、物体の位置
はFinslerの時間距離を決めるので、物体の位置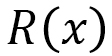 と同じように、座標関数と呼んでいます。
と同じように、座標関数と呼んでいます。
このような対応から、
- 1次元弾性エネルギーの線積分
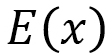 に、液晶分子の向きに関連した異方性がうまく取り込める
に、液晶分子の向きに関連した異方性がうまく取り込める - その異方的になった1次元弾性エネルギーから、Finslerの時間距離を求め、その計量関数を求める
- これを他の2方向に対しても行う
ことができれば、3次元の異方的なハミルトニアンが得られる、と考えられます。この目的のため、Finsler関数を、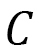 軸上の
軸上の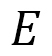 と
と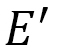 をつかって、
をつかって、
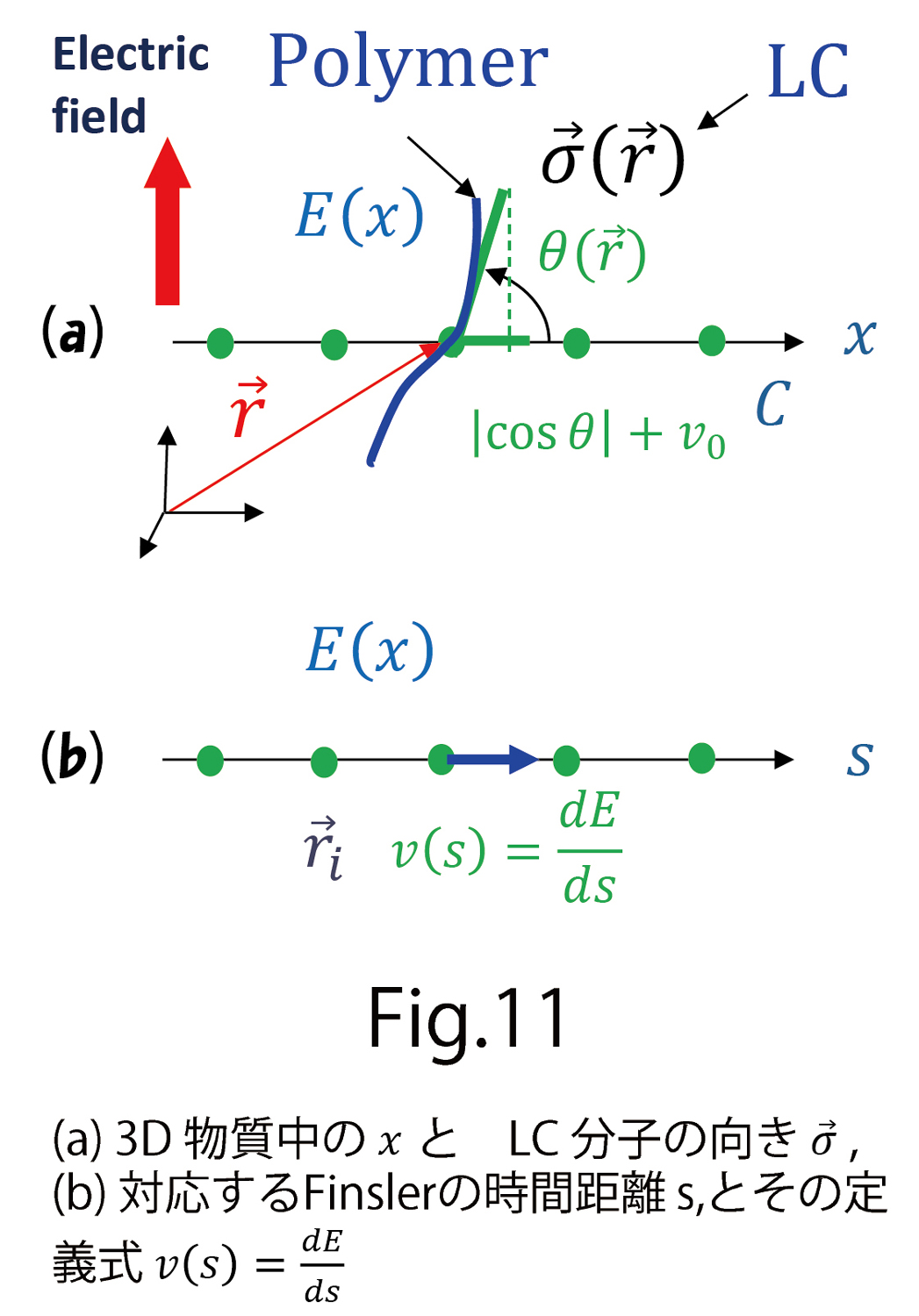
(C-6)
と定義します(図11(a))。図11(a)は図8の軸を拡大した図です。ここで問題は、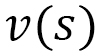 です。
です。
図11(a)のようにポリマーが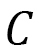 軸に垂直になっているような場合は
軸に垂直になっているような場合は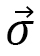 と
と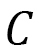 軸の角度は
軸の角度は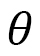 大きく
大きく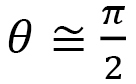 なり、逆にポリマーが
なり、逆にポリマーが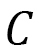 軸と平行になっているような場合は
軸と平行になっているような場合は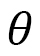 は小さく
は小さく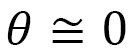 なります。そこで
なります。そこで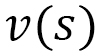 を
を
(C-7)
と定義します。ここで、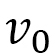 は小さな正数
は小さな正数 です。もし、
です。もし、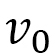 が
が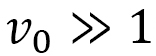 のような数だったら、
のような数だったら、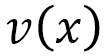 は定数になり、その時は
は定数になり、その時は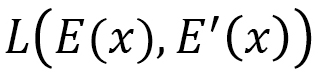 から定まる距離sは普通の距離になり、異方性は現れません。この意味で、
から定まる距離sは普通の距離になり、異方性は現れません。この意味で、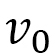 は異方性の強さを表すパラメータともいえます。
は異方性の強さを表すパラメータともいえます。
さて、次の問題はこのようにして得られたFinsler関数から、どうやって、異方的な弾性エネルギーを求めるか、ということです。そのために、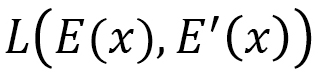 から計量関数 g (Finsler計量)を、公式によって求めると
から計量関数 g (Finsler計量)を、公式によって求めると
(C-8)
となります。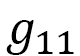 と書いたのは、この
と書いたのは、この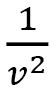 は3行3列のgの(1,1)成分ということです。その意味は、
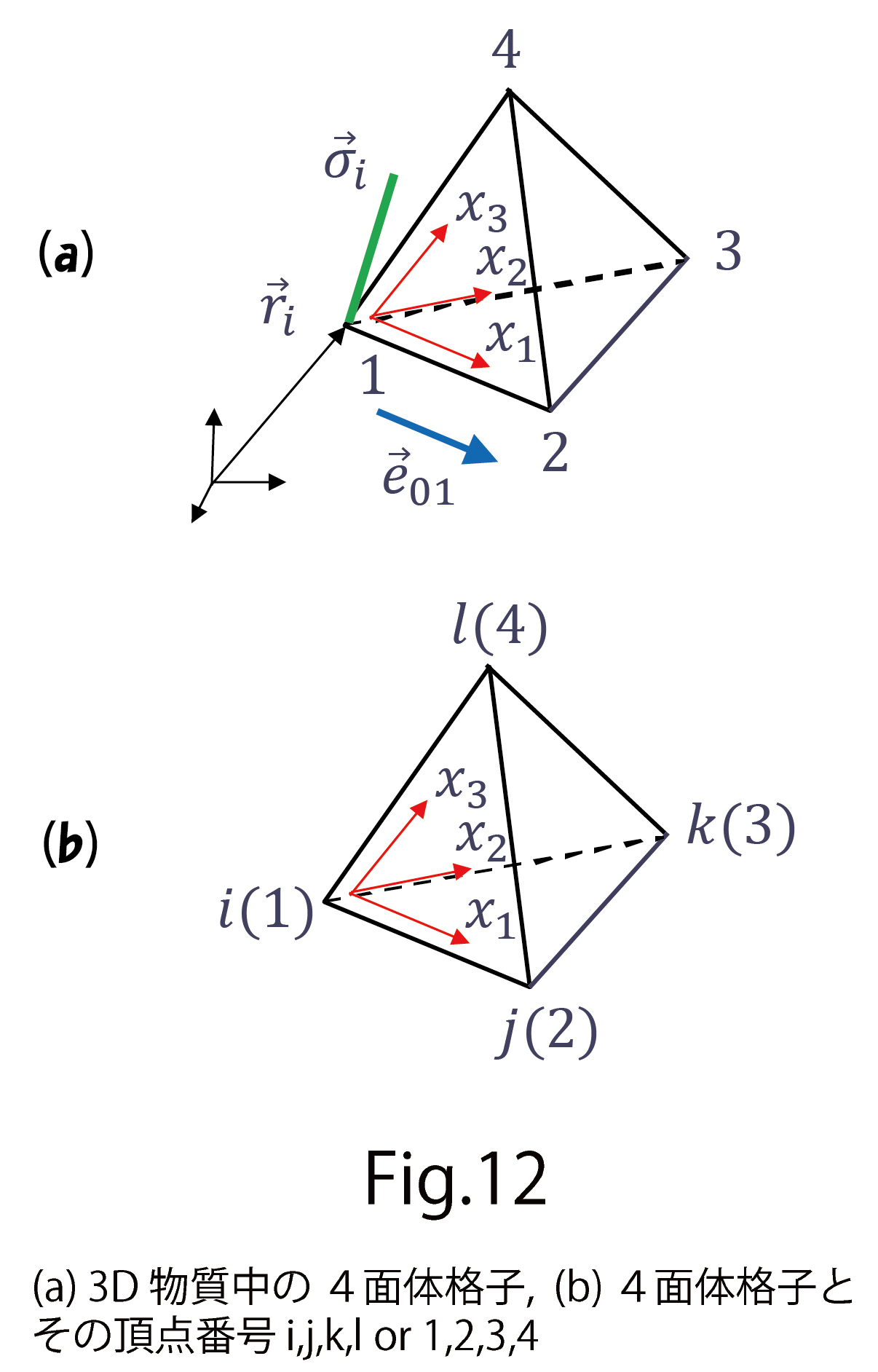
は3行3列のgの(1,1)成分ということです。その意味は、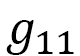 は図12(a)に示したような局所座標系の
は図12(a)に示したような局所座標系の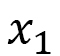 軸に対応する要素ということです。ここで、
軸に対応する要素ということです。ここで、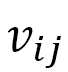 は図のように
は図のように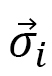 と単位方向ベクトル
と単位方向ベクトル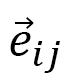 から
から
(C-9)
のように求まり、Finsler計量は
(C-10)
となります。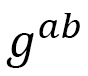 は逆行列、
は逆行列、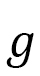 は行列式です。このようにして求めたFinsler計量を、一般の座標系で書かれたハミルトニアン
は行列式です。このようにして求めたFinsler計量を、一般の座標系で書かれたハミルトニアン
(C-11)
に代入することで、液晶分子の向きに由来した異方性が取り込まれるはずです。詳細は省きますが、4面体で分割した図12(a)のような4面体の3次元格子上で式(C-11)を離散化しますと
(C-12)
となります。ここで、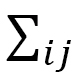 、
、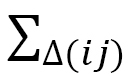 はボンドij、ボンドijを共有する4面体
はボンドij、ボンドijを共有する4面体 に関する和、
に関する和、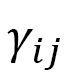 は図12(b)の4面体ijklにおける辺ij上で定義されたものです。このHはまた
は図12(b)の4面体ijklにおける辺ij上で定義されたものです。このHはまた
(C-13)
のように、4面体に関する和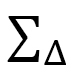 とその4面体
とその4面体 に含まれるボンドijの和
に含まれるボンドijの和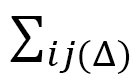 を使っても表わされます。
を使っても表わされます。
ここで、問題はこのようにして得られたFinsler計量を使えば、望みの異方的な性質が確かに得られるかどうかです。これは、定性的には次のようにして、分かります。
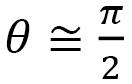 の場合:
の場合:
これは図11(a)の 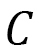 軸上で、1次元弾性エネルギー
軸上で、1次元弾性エネルギー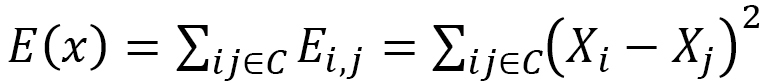 と
と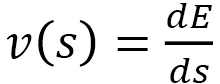 から
から
(C-14)
が得られるので、積分すると
(C-15)
となります。ただし、 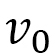 は小さな数であることを仮定しています。左辺は
は小さな数であることを仮定しています。左辺は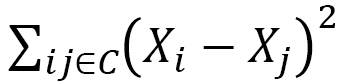 なので、 結局、
なので、 結局、
(C-16)
となり、これは、電場と垂直方向のモノマー間距離は小さくなるということを表わしています。
さらに、弾性エネルギーは張力定数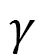 をかけたものになること、その弾性エネルギーは全体として一定になることを考えると、
をかけたものになること、その弾性エネルギーは全体として一定になることを考えると、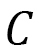 軸上で、
軸上で、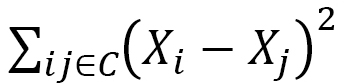 が減少するということは、この方向に関しては 有効ばね定数 が大きくなることを意味します。すなわち、 電場による異方的変形の原因は、分子間力が動的に変化するためということになります。”分子間力が動的に変化するように見える”が正しいかもしれません。
が減少するということは、この方向に関しては 有効ばね定数 が大きくなることを意味します。すなわち、 電場による異方的変形の原因は、分子間力が動的に変化するためということになります。”分子間力が動的に変化するように見える”が正しいかもしれません。
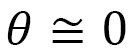 の場合:
の場合:
これは図8のY軸でみた場合です。 上記の1次元弾性エネルギーに対する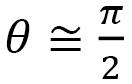 の場合と同様の考察から、
の場合と同様の考察から、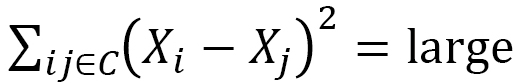 という結果が得られることはすぐにわかります。これは、液晶エラストマは電場と同じ向きには延びるということを表わしています。
という結果が得られることはすぐにわかります。これは、液晶エラストマは電場と同じ向きには延びるということを表わしています。
C-2.液晶エラストマ(LCE)の電場応答(文献[3,4])
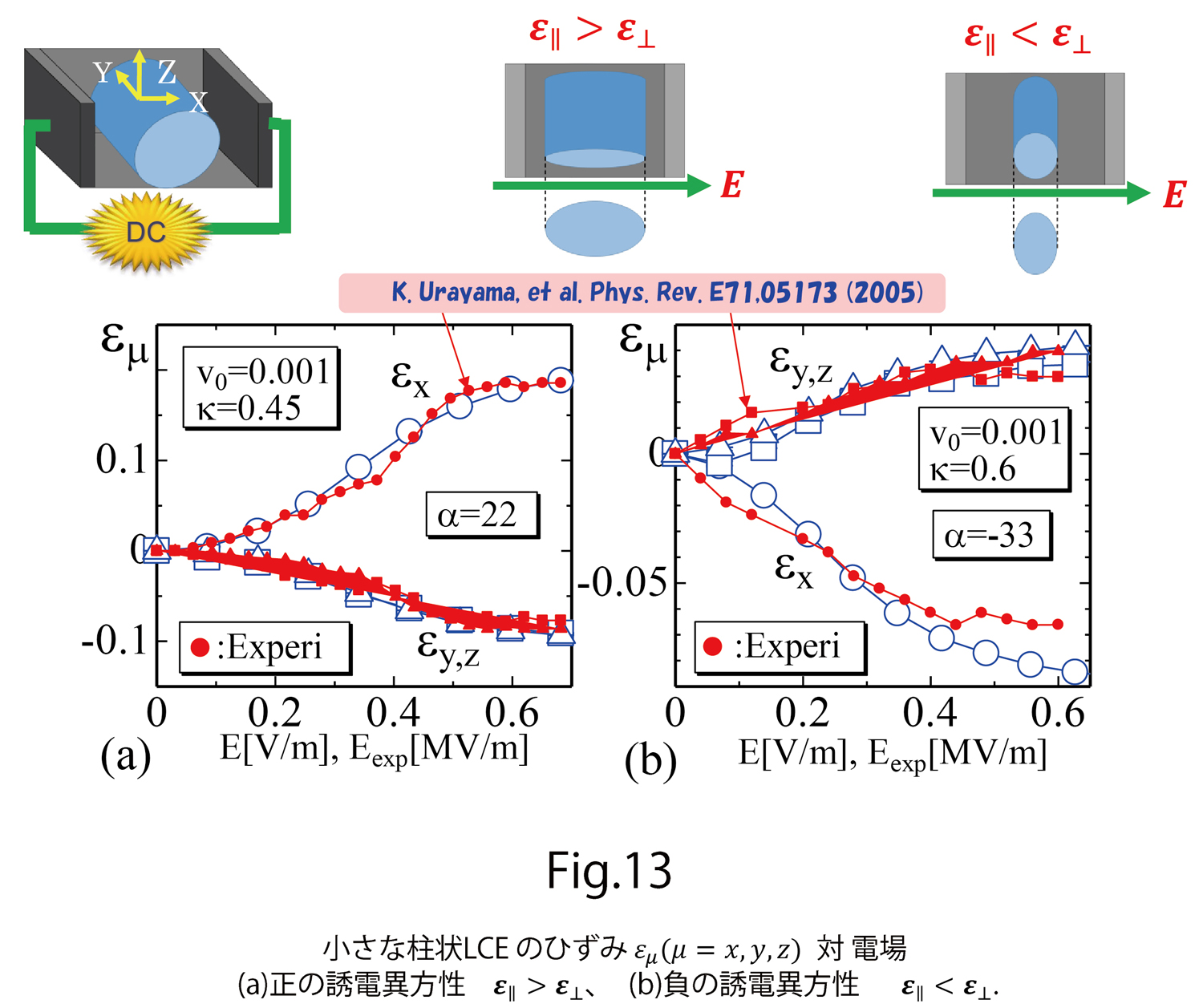
ここでは、電場応答の計算結果のいくつかを説明します。図13は、文献[5]で報告された実験結果と計算結果:ひずみ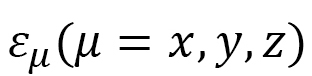 対電場
対電場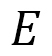 をplotしたものです。小さな円柱状のLCEに電場をかけた時に起こる変形のひずみを3方向で測定した実験結果と一緒に、計算結果を示しています。図13(a)は誘電異方性が正
をplotしたものです。小さな円柱状のLCEに電場をかけた時に起こる変形のひずみを3方向で測定した実験結果と一緒に、計算結果を示しています。図13(a)は誘電異方性が正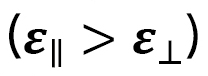 の場合、即ち、電場方向に延びる場合で、図13(b)は負
の場合、即ち、電場方向に延びる場合で、図13(b)は負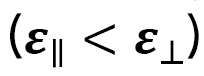 の場合です。計算に用いたパラメータの詳細はここでは省略しますが、計算結果は実験結果とよく一致していることが分かります。
の場合です。計算に用いたパラメータの詳細はここでは省略しますが、計算結果は実験結果とよく一致していることが分かります。
図14は誘電異方性が正の場合の計算結果のアニメーションです。見やすくするために、アニメーションのひずみは実際のひずみよりも大きくなっています。電場が大きくなると、液晶分子の向き(赤い小さな棒)が電場方向に整列し、同時に物体全体が変形していくことが分かります。
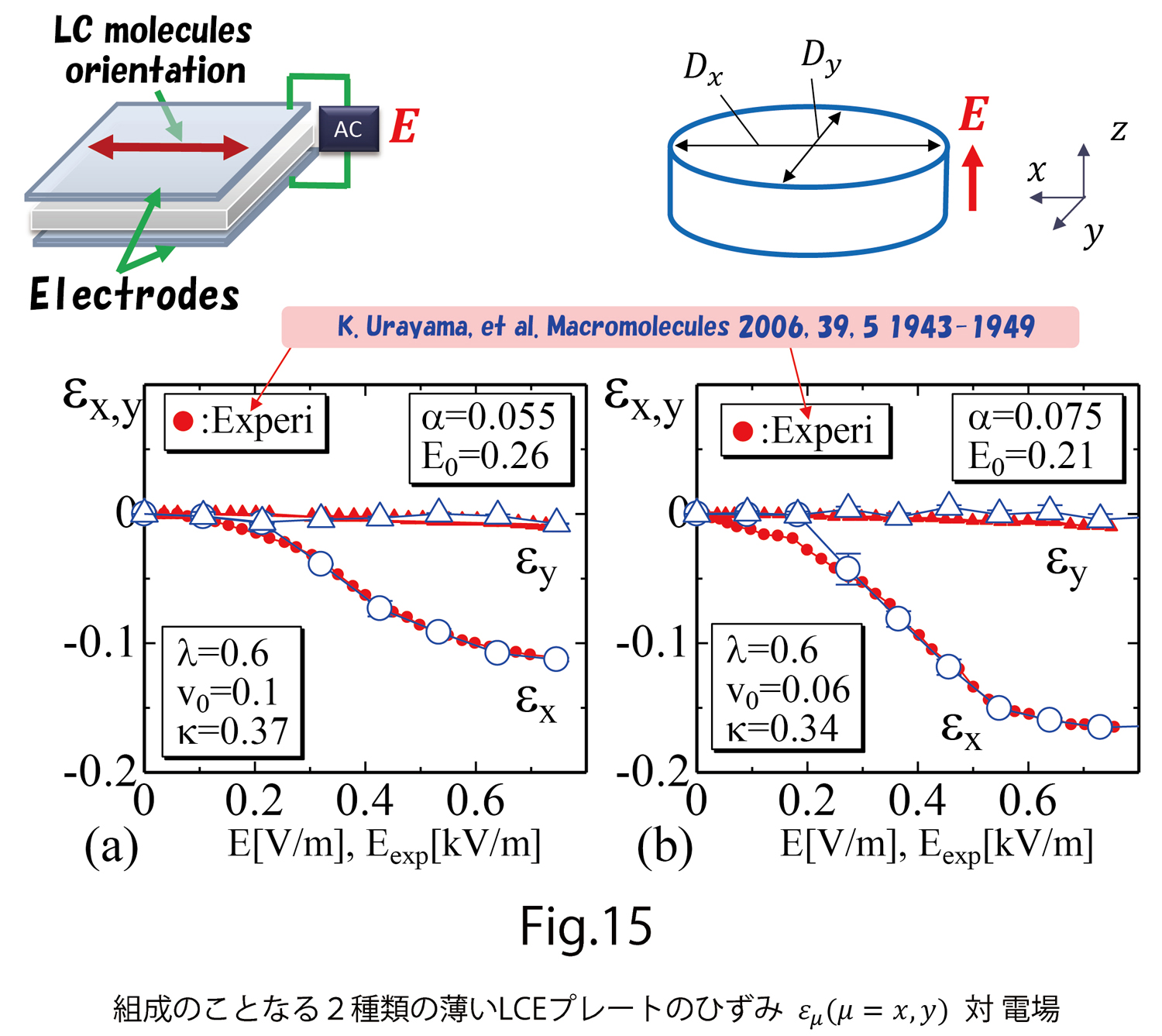
図15は、文献[6]で報告された実験結果と筆者らの計算結果をplotしたものです。文献[6]の実験結果は、薄い板状のLCEの面内のひずみ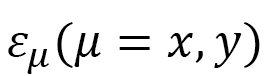 を測定したものです。また、このLCEははじめから、図15の上部に示すような向き(x軸方向)に液晶分子が配向しているものです。この状態で、z方向に電場をかけると、その電場が大きくなると、液晶分子の向きはz軸方向に向いていきます。従って、液晶分子のy軸方向の向きは変わらないので、y方向には変形が起こりません。z軸方向にも厚みは変化しますが、大きく変形するのはx方向です。数値計算結果は、このような実験結果をよく再現しています。
を測定したものです。また、このLCEははじめから、図15の上部に示すような向き(x軸方向)に液晶分子が配向しているものです。この状態で、z方向に電場をかけると、その電場が大きくなると、液晶分子の向きはz軸方向に向いていきます。従って、液晶分子のy軸方向の向きは変わらないので、y方向には変形が起こりません。z軸方向にも厚みは変化しますが、大きく変形するのはx方向です。数値計算結果は、このような実験結果をよく再現しています。
図16は変形の様子を表わすアニメーションです。この場合も、見やすくするため、アニメーションの変形は実際の変形より大きくしています。確かにy方向には変形していないことが分かります。
- 文献[5] K. Urayama, et al. Electrically driven deformations of nematic gels, Phys. Rev. E71, 05173 (2005)
- 文献[6] K. Urayama, et al. Deformation Coupled to Director Rotation in Swollen Nematic Elastomers under Electric Fields, Macromolecules 2006, 39, 5 1943-1949




D.最近の研究成果
以下では、最近の研究で得られた結果を示します。
D-1.磁気スキルミオンの機械的応力による異方的変形(文献[7])
磁気スキルミオンとは、カイラル磁石と呼ばれる種類の磁石に、ある条件の下で発生する安定なスピンの状態のことです。この安定性のために、将来の磁気メモリへの応用が期待されています。
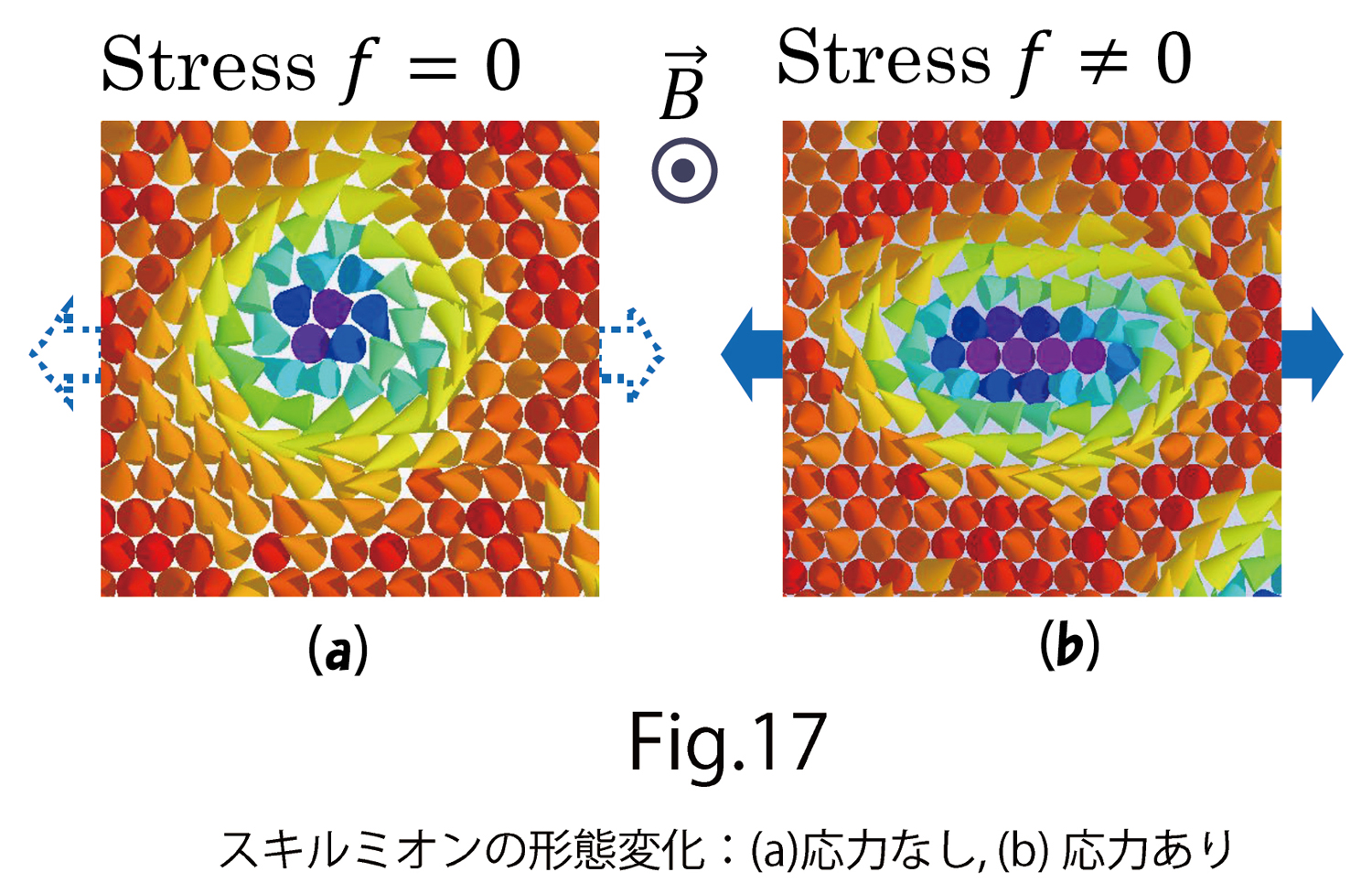
少し前になりますが、カイラル磁石に機械的な外力または応力をかけたときに、スキルミオンの状態が大きく変化する(図17)ことが、理論的にも指摘されていましたが、実験的にも報告されました(文献[8])。その材料に引っ張り応力を加えるとスキルミオンの形が円形から楕円形に変化するという結果です。スキルミオンは電子の状態を表わしているので、なぜ機械的な刺激がスキルミオンに影響するのかは不思議です。
この円から楕円への変形というのを異方的な変形とみれば、液晶エラストマーの時と同じ考え方で、説明できるのではないかと考えられます。磁気スキルミオンは2つの相互作用が競合してその結果発生すると考えられています。それはスピン間の強磁性相互作用(FMI)とジャロシンスキー・守谷相互作用(DMI)です。簡単のため、ここでは2次元としますと、FMIとDMIはそれぞれ次のようになります:
(D-1)
これらも、前と同じく、一般の曲線座標系の計量行列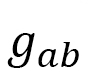 を使って書いています。Euclid計量
を使って書いています。Euclid計量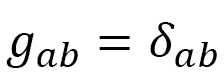 (2行2列の単位行列)の場合、これらは
(2行2列の単位行列)の場合、これらは
(D-2)
となります。ここで、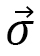 は単位球面上に値を持つ単位ベクトルで電子スピンを表わし、
は単位球面上に値を持つ単位ベクトルで電子スピンを表わし、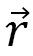 はそのスピンの位置を表わします。
はそのスピンの位置を表わします。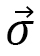 は変数ですが、
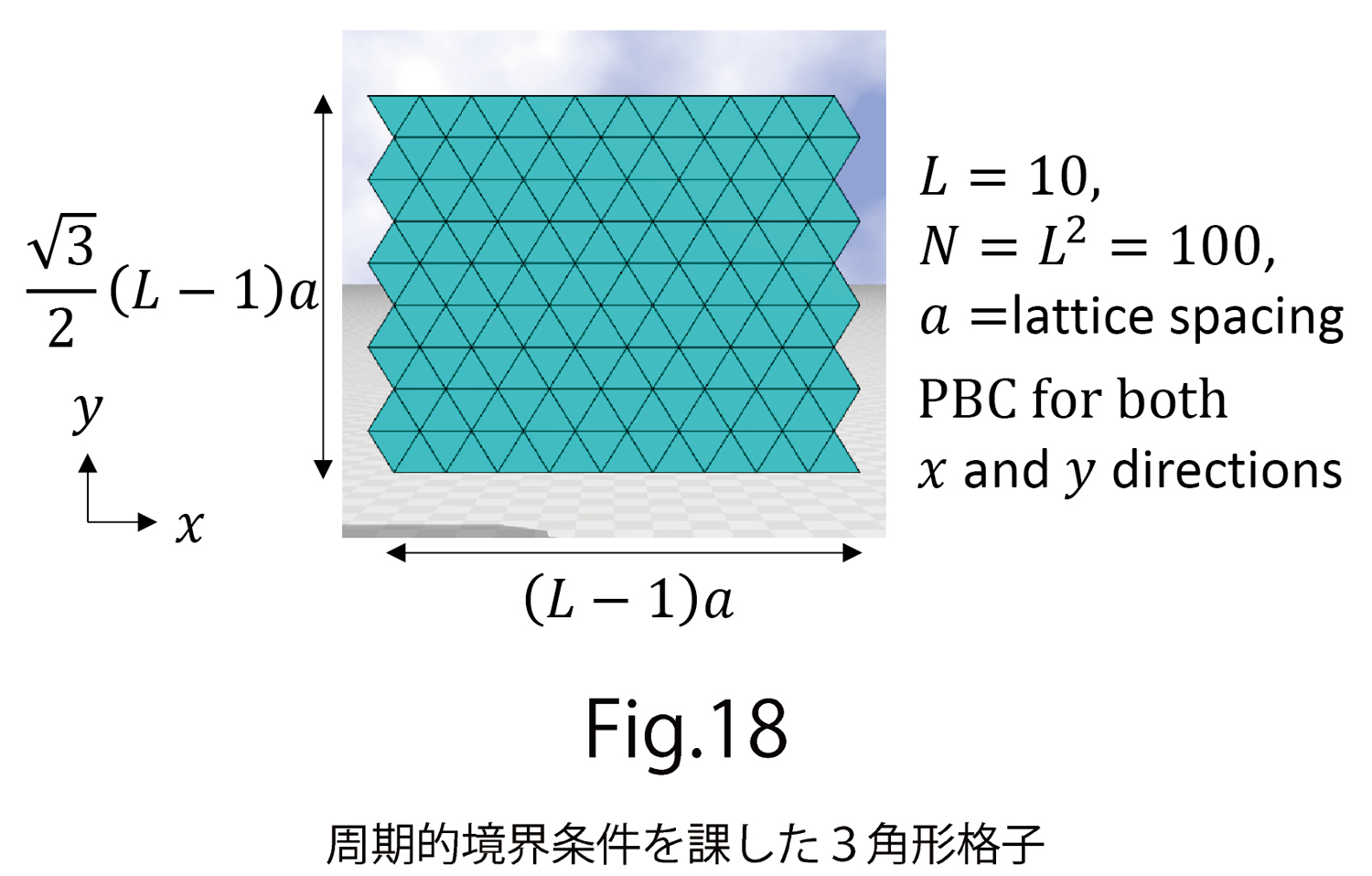
は変数ですが、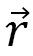 は固定です。これらのハミルトニアンは、数値計算するために、格子上で離散化します。4角形格子が普通多く使われますが、ここでは3角形格子で説明します(図18)。離散化したものは次のようになります:
は固定です。これらのハミルトニアンは、数値計算するために、格子上で離散化します。4角形格子が普通多く使われますが、ここでは3角形格子で説明します(図18)。離散化したものは次のようになります:
(D-3)
ここで、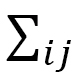 は隣り合う格子点
は隣り合う格子点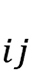 に関する和、
に関する和、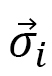 は格子点
は格子点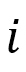 におけるスピン、
におけるスピン、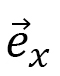 は格子点
は格子点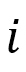 から
から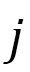 に向かう単位ベクトル、を表わします。全ハミルトニアンは
に向かう単位ベクトル、を表わします。全ハミルトニアンは
(D-4)
となります。ここで,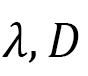 はFMI定数,DMI定数,
はFMI定数,DMI定数,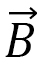 は磁場を表わします。
は磁場を表わします。
- 文献[7]:S.El Hog, et al. Phys. Rev. B. 104,024402 (2021) https://doi.org/10.1103/PhysRevB.104.024402
- 文献[8]:K.Sahibata et al. Nature Nanotech. 10, 589-592(2015)
さて、カイラル磁石を引っ張るときに現れるスキルミオンの異方的変形に対し、
- 異方的変形の原因となる内部自由度は何か?
- FMIとDMIのどちらにFinsler計量を仮定すればよいか?
という問題を考える必要があります。
- に関しては、原子の位置のずれが関係すると予想されるので、そのずれ方向を表わす「ひずみ場」として単位ベクトル
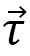 を考えます。
を考えます。 - に関しては、文献[8]でもDMIの異方性が指摘されているため、DMIにFinsler計量を適用します。文献[7]ではFMIとDMIの両方に適用した計算結果が示されていますが、ここではDMIについてのみ説明します。
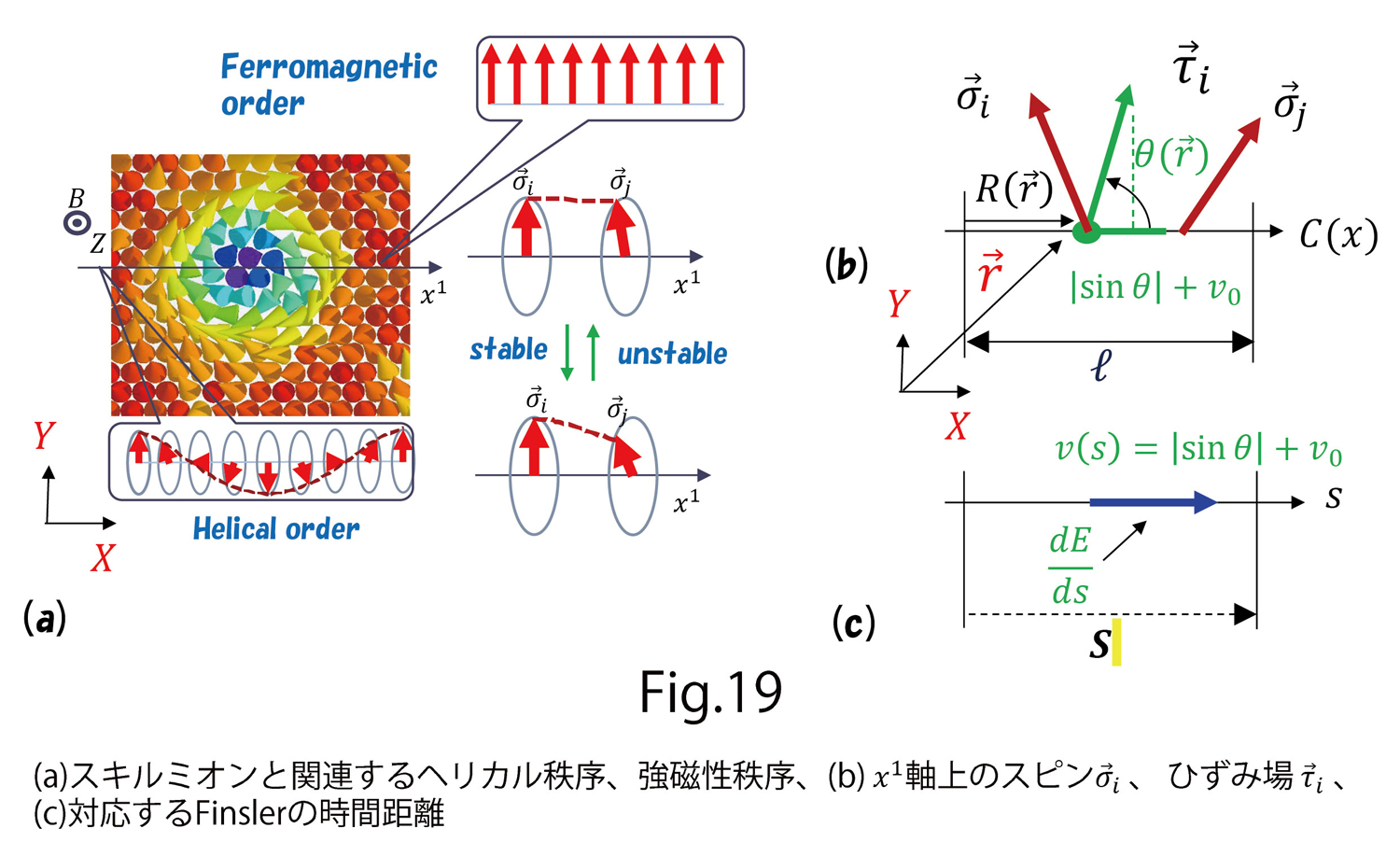
さて、図19(a)の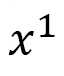 軸のようなスキルミオンの中心をとおる軸を考えます。この軸に沿って、図のようにHelical orderと呼ばれる状態が発生してます。同時に、図19(a)には見えませんが隣のスキルミオンとの間にferromagnetic orderも発生しています。そこで、この
軸のようなスキルミオンの中心をとおる軸を考えます。この軸に沿って、図のようにHelical orderと呼ばれる状態が発生してます。同時に、図19(a)には見えませんが隣のスキルミオンとの間にferromagnetic orderも発生しています。そこで、この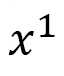 軸上で
軸上で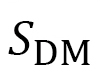 のX軸(=
のX軸(=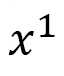 軸)成分を積分したものとその導関数
軸)成分を積分したものとその導関数
(D-5)
を考えます(図19(b)) 。負号は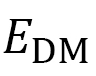 が正になるようにするためです(文献[9])。ここで、Finsler関数
が正になるようにするためです(文献[9])。ここで、Finsler関数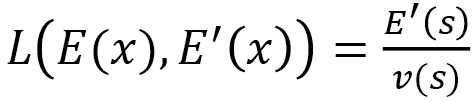 の
の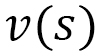 としては
としては
(D-6)
を考えます(図19(c))。今度は、cosでなくsinになります。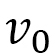 は前と同じく小さな正数です。
は前と同じく小さな正数です。
ここで、Finslerの距離sは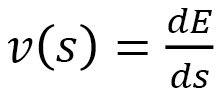 によって定義されることを考えると、引っ張り応力がX軸方向にかかるとひずみ場
によって定義されることを考えると、引っ張り応力がX軸方向にかかるとひずみ場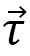 はX軸と平行になるので、
はX軸と平行になるので、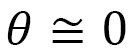 即ち
即ち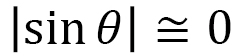 となって
となって
(D-7)
となり、極小になります。従って、積分したものは
(D-8)
となります。このことは、図19(a)のHelical orderが不安定化することを意味します。X軸上で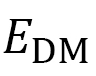 が小さくなるということは、2次元の
が小さくなるということは、2次元の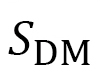 で考えれば、この軸上でDMI定数が小さくなるということです。
で考えれば、この軸上でDMI定数が小さくなるということです。
次元解析からも説明できます。次元解析から FMI定数/DMI定数=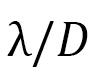 が大きい(小さい)ときスキルミオンも大きく(小さく)なります。 FMI定数は一定なので、X軸上でDMI定数が小さくなるということから、X方向にスキルミオンの形が伸びることが分かります。
が大きい(小さい)ときスキルミオンも大きく(小さく)なります。 FMI定数は一定なので、X軸上でDMI定数が小さくなるということから、X方向にスキルミオンの形が伸びることが分かります。
- 文献[9]:S.El Hog, et al. AirXiv http://arxiv.org/abs/2112.02173
次は、2次元の計量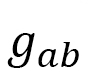 を求めて、2次元の離散的ハミルトニアンを求めます。
を求めて、2次元の離散的ハミルトニアンを求めます。
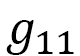 は、今考察してきたX軸を局所座標系の
は、今考察してきたX軸を局所座標系の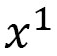 軸とみれは、公式から
軸とみれは、公式から
(D-9)
となります。 2次元のFinsler計量は
(D-10)
となります。 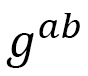 は逆行列、
は逆行列、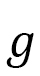 は行列式で、前と同じです。ここで、
は行列式で、前と同じです。ここで、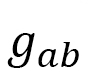 における
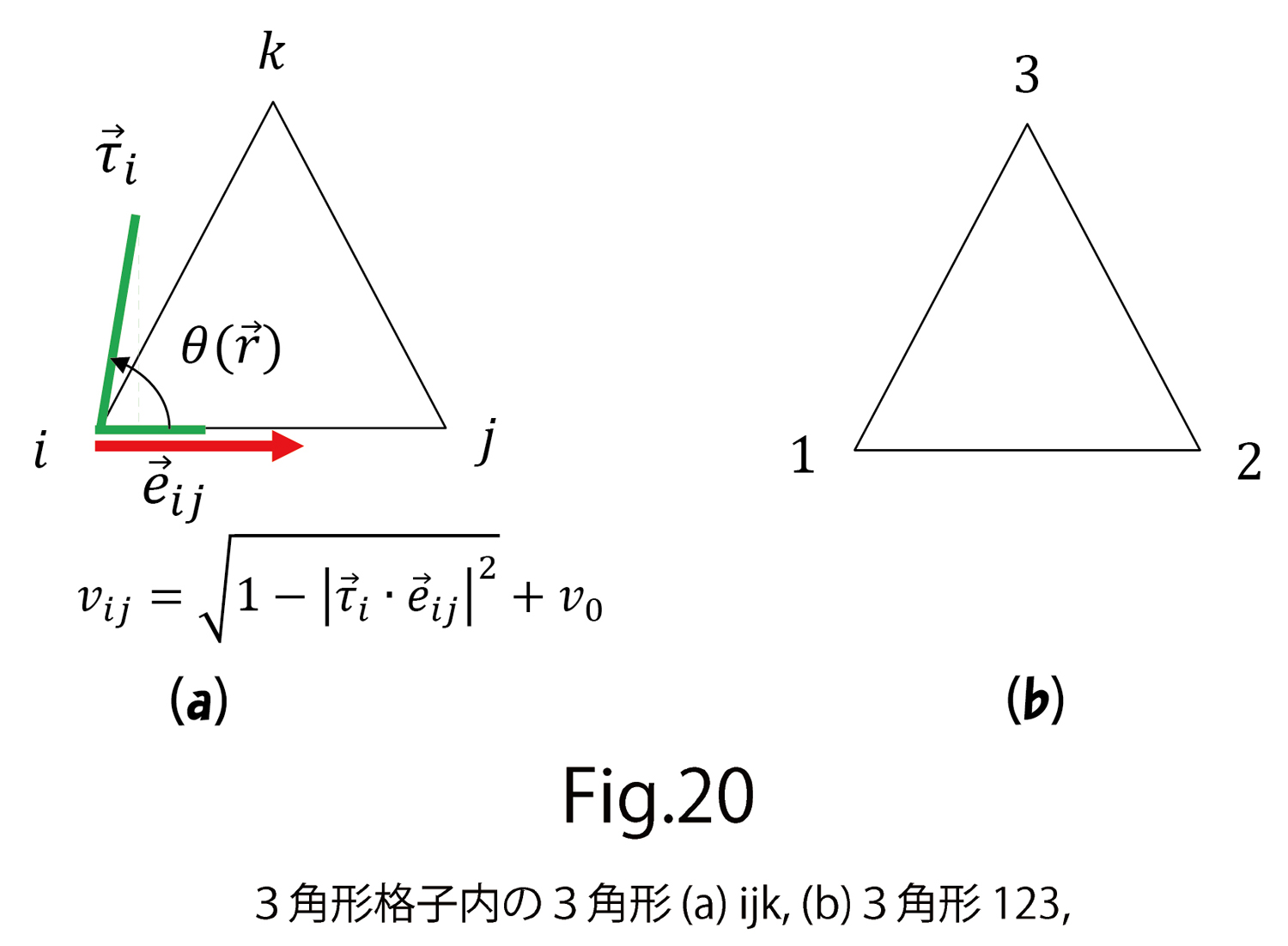
における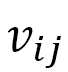 は図20(a)のようにひずみ場
は図20(a)のようにひずみ場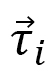 と単位方向ベクトル
と単位方向ベクトル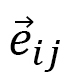 から
から
(D-11)
のように求まります。ここで、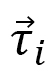 は2つの軸に共通ですが、
は2つの軸に共通ですが、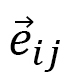 は異なっているので、
は異なっているので、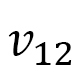 と
と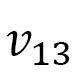 は異なっています。
は異なっています。
このようにして求めたFinsler計量を、一般の座標系で書かれた式(D-1)のハミルトニアン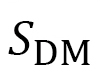 に代入します。このとき、
に代入します。このとき、
(D-12)
のような置き換えをします。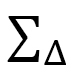 は3角形に関する和を表わします。
は3角形に関する和を表わします。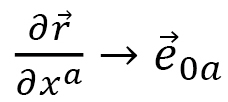 に関しては、
に関しては、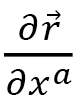 はここでは単位長さのベクトルに置き換えています。従って
はここでは単位長さのベクトルに置き換えています。従って
(D-13)
が得られます。この3角形123において座標原点としては頂点1だけでなく、頂点2でも頂点3でも構いません(図20(b))。そこで、すべての可能な座標原点からの寄与を考慮するという考えのもと、添え字に関して1→2, 2→3, 3→1のような入れ替えをして、他の2種類の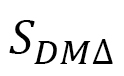 を加えて、係数1/3をかけるというような、対称化を行いますと、
を加えて、係数1/3をかけるというような、対称化を行いますと、
(D-14)
のように、3角形の頂点の番号123を使って表わされます。3角形の頂点を123の代わりに一般的に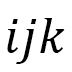 を使いますと
を使いますと
(D-15)
のように表わされます。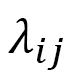 はある3角形
はある3角形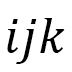 の辺
の辺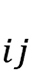 で定義された有効DM相互作用定数と解釈できます。
で定義された有効DM相互作用定数と解釈できます。
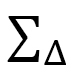 で3角形
で3角形 の和を取ると、各辺ijに対して2回ずつ
の和を取ると、各辺ijに対して2回ずつ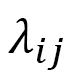 が現われます。そのようにして現れるもう一つの
が現われます。そのようにして現れるもう一つの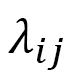 は上記の
は上記の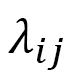 とは異なり、少し複雑ではあります。しかし、重要な点は、式(D-11)の
とは異なり、少し複雑ではあります。しかし、重要な点は、式(D-11)の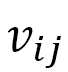 によって導入された異方性が、有効DM相互作用定数としてモデルに組み込まれるということです。
によって導入された異方性が、有効DM相互作用定数としてモデルに組み込まれるということです。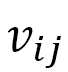 はもともとFinsler関数によって
はもともとFinsler関数によって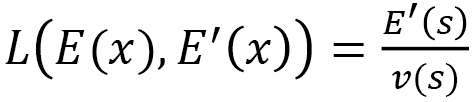 のように導入され、このLから計量を求めて、その計量をハミルトニアンの離散化に用いたわけですが、その計量は
のように導入され、このLから計量を求めて、その計量をハミルトニアンの離散化に用いたわけですが、その計量は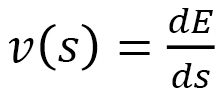 で定義されるFinslerの時間距離sにおける長さを決めるものです。即ち、材料内部を Finslerの時間距離sに支配されたものとみることで、異方性を持った有効DM相互作用定数が求まるということです。
で定義されるFinslerの時間距離sにおける長さを決めるものです。即ち、材料内部を Finslerの時間距離sに支配されたものとみることで、異方性を持った有効DM相互作用定数が求まるということです。
次に計算結果のいくつかを示します。
図21(a)には、磁場B-温度Tの相図を示します。3種類のskyrmion(sky)相、ferromagnetic(ferro)相、stripe相と、その中間のskyrmion-stripe(sk-st)相、skyrmion-ferromagnetic(sk-fe)相、の5つに分類しています。X軸方向に応力を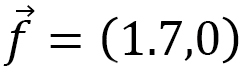 のようにかけていますので、図21(b)からも分かりますようにskyrmionはX軸方向に細長く伸びています。縦と横の長さを図21(c)のように数値的に測定して、縦横の長さ
のようにかけていますので、図21(b)からも分かりますようにskyrmionはX軸方向に細長く伸びています。縦と横の長さを図21(c)のように数値的に測定して、縦横の長さ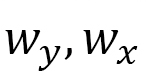 から、その形状異方性
から、その形状異方性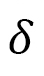 を
を
(D-16)
で計算し、ヒストグラムを求めます。そうすると、図21(d)のように、文献[8]に報告されている実験結果とほぼ一致しています。
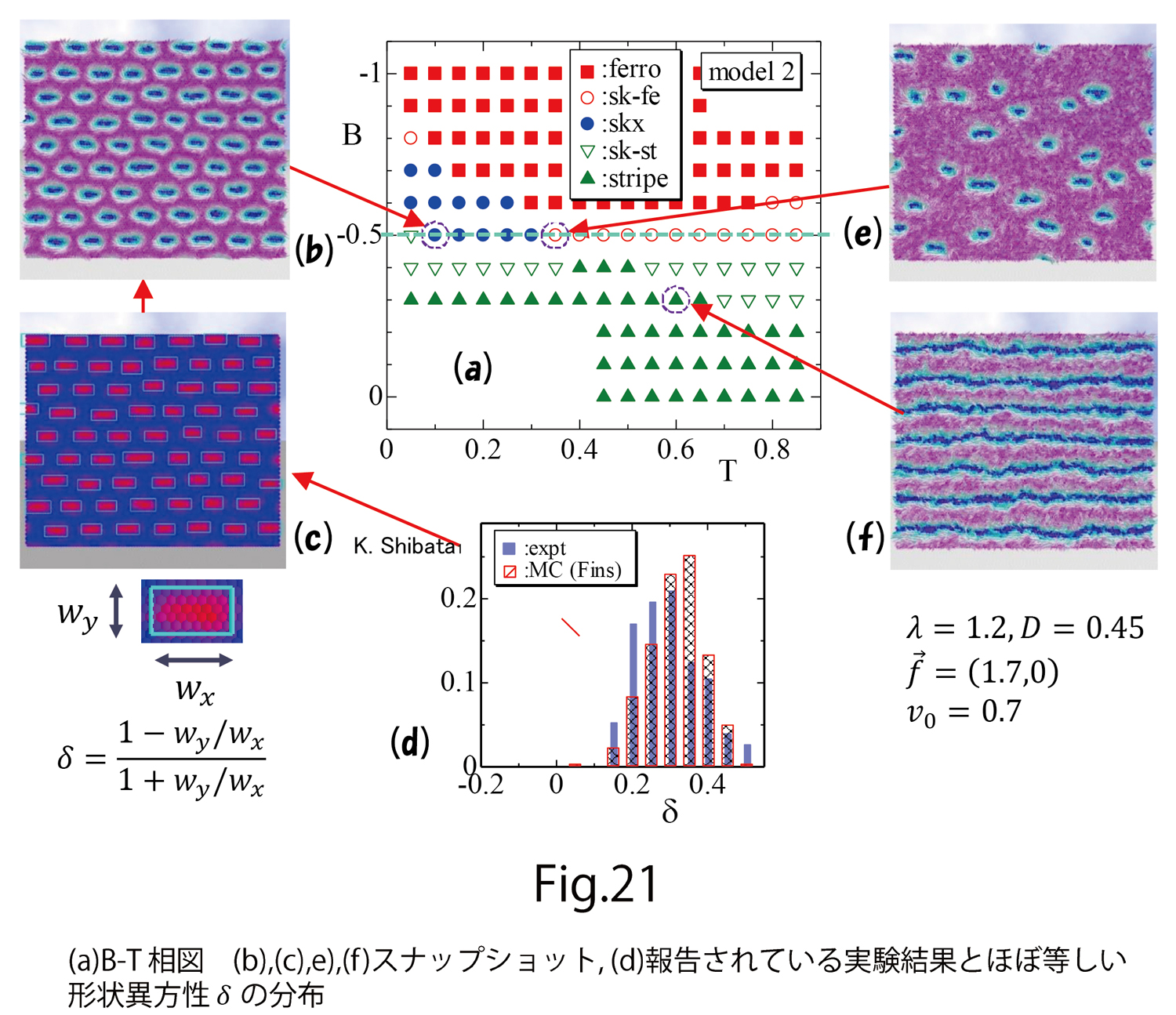
図22(a)には、(D-15)に与えられている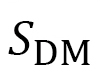 から1分子当たりのDM相互作用エネルギー
から1分子当たりのDM相互作用エネルギー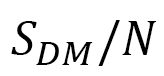 とFM相互作用エネルギー
とFM相互作用エネルギー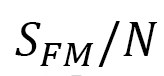 をplotしています。ここで、
をplotしています。ここで、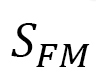 は次のように定義されています。
は次のように定義されています。
(D-17)
図22(a)の両側矢印の温度領域がスキルミオンです。温度の上昇とともに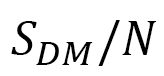 の値は絶対値が減少しているのは、スキルミオンが不安定化することを表わします。逆に、FM相互作用エネルギー
の値は絶対値が減少しているのは、スキルミオンが不安定化することを表わします。逆に、FM相互作用エネルギー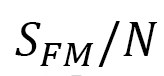 は、スキルミオンの温度領域で減少していて、ferromagnetic orderとしては安定化に向かっていることが分かります。この2つのエネルギーの一方が安定化(不安定化)すると他方が不安定化(安定化)するのは競合という原理です。
は、スキルミオンの温度領域で減少していて、ferromagnetic orderとしては安定化に向かっていることが分かります。この2つのエネルギーの一方が安定化(不安定化)すると他方が不安定化(安定化)するのは競合という原理です。
図22(b)には、 式(D-15)の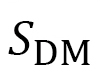 における、相互作用定数の異方性
における、相互作用定数の異方性
(D-18)
をplotしています。ここで、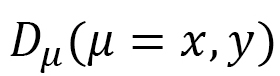 は
は
(D-19)
のようになります。ここで、和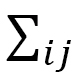 はボンドijの両側にある2つの3角形からの寄与を考慮しています。
はボンドijの両側にある2つの3角形からの寄与を考慮しています。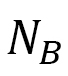 はボンドの総数です。
はボンドの総数です。
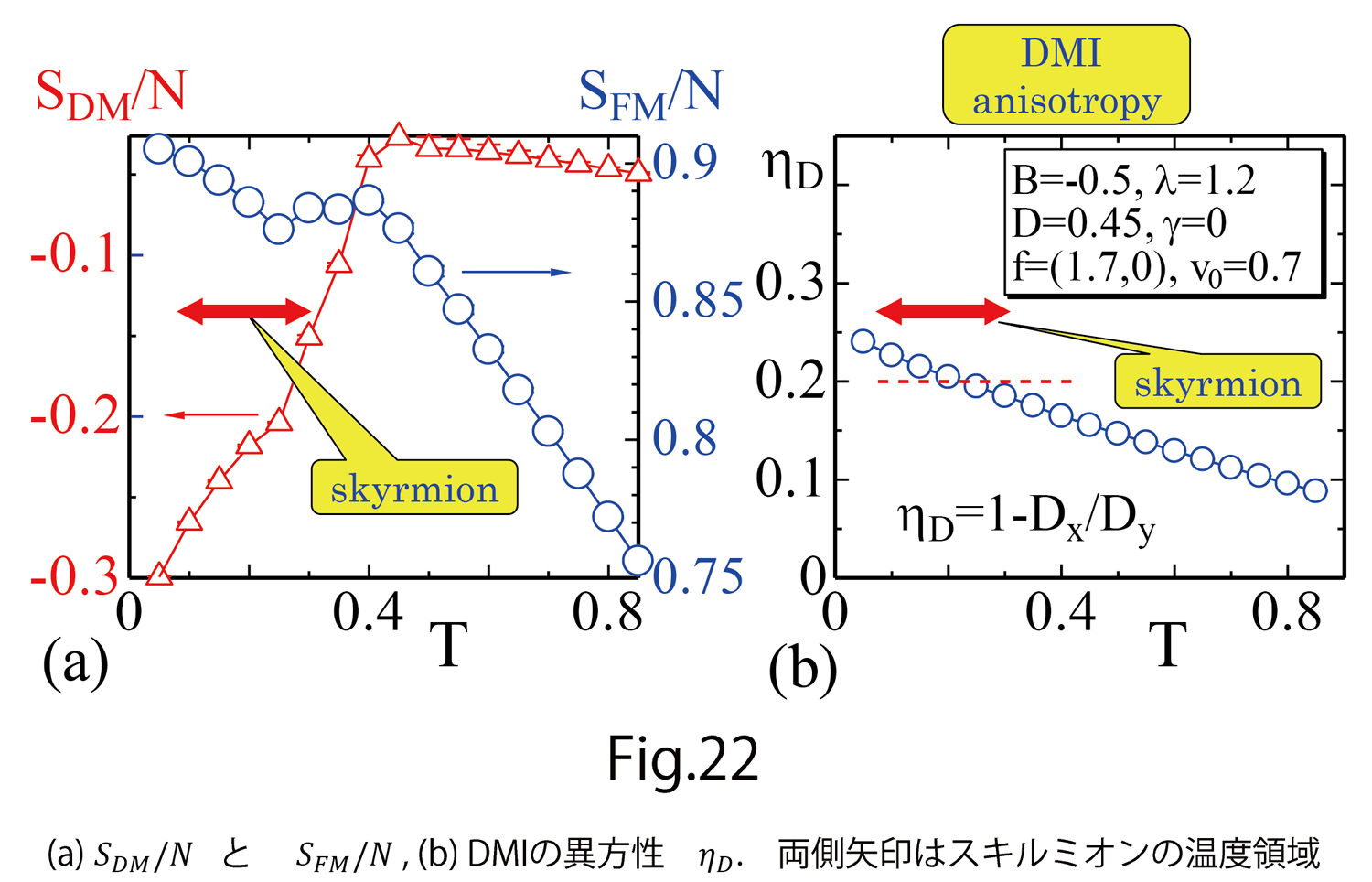
相互作用定数の異方性は、スキルミオンの温度領域で、0.2程度の値になっています。これは、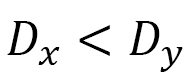 を意味します。X軸方向に相互作用定数が小さくなっていることは、(D-8)のところの議論の結果と一致します。注目すべきことは、図22(b)で赤い点線を引いたところは
を意味します。X軸方向に相互作用定数が小さくなっていることは、(D-8)のところの議論の結果と一致します。注目すべきことは、図22(b)で赤い点線を引いたところは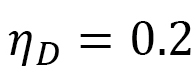 ですが、この値は、文献[8]で報告された数値計算においてスキルミオンがX軸上に細長くなるように仮定されたDMIの異方性と同じ値です。ここでは、図21(a)から、
ですが、この値は、文献[8]で報告された数値計算においてスキルミオンがX軸上に細長くなるように仮定されたDMIの異方性と同じ値です。ここでは、図21(a)から、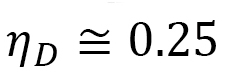 位で実験結果と一致しますので、全く同じ値ではないですが、ほぼ近い値になります。
位で実験結果と一致しますので、全く同じ値ではないですが、ほぼ近い値になります。
D-2.強誘電体ポリマーPVDFの電場による変形(文献[10])
強誘電体といえば、チタン酸バリウム BaTiO3 といったセラミクス強誘電体が知られています。強誘電体は電場をかけると誘電分極する物質で、その電場を取り除いても分極したままになるような物質です。このため、応用上からも、盛んに研究されています。
さて、PVDF、はポリフッ化ビニリデンと呼ばれる強誘電体であってポリマーである物質で、H.Kawaiの研究(文献[11])が有名です。その特徴は、セラミクス強誘電体に比べて電場による変形ひずみが大きいことでぉ;す。このことから、アクチュエータなどの応用上の観点で非常に興味を持たれている物質です。
このPVDFはポリマーなので、その基本的なハミルトニアンは液晶エラストマーの場合と同じく、ガウシアンボンドポテンシャルです。液晶エラストマーとの違いは異方性をもたらす内部自由度だけです。PVDFでは内部自由度は誘電体の分極ベクトルです。分極ベクトルは液晶分子の向きと違って極性を持ちますから、本質的な違いは内部自由度が非極性か極性かだけです。
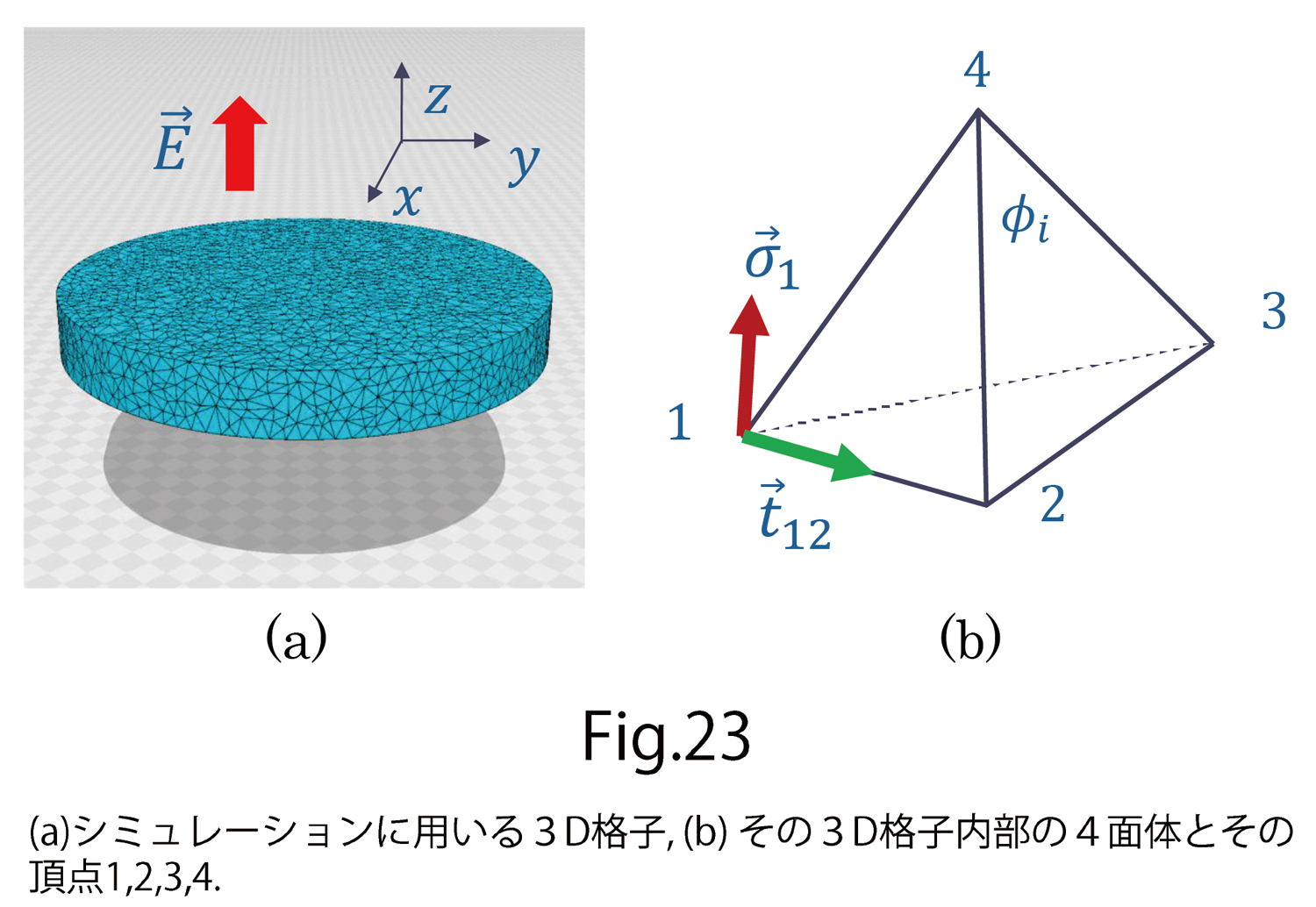
数値計算では図23(a)のような3次元格子を使って、電場をdisk面と垂直なZ軸方向にかけたとき、Z軸方向にひずみと分極の値を計算し、報告されている実験結果と比べます。この3次元diskは図23(b)のような4面体格子で分割されていることも、液晶エラストマーの場合と同じです。
異方性の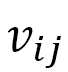 としては
としては
(D-20)
とします。これは、分極ベクトル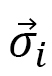 と局所座標軸との角度が
と局所座標軸との角度が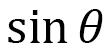 の場合なので、形としてはスキルミオンの場合と同じです。3次元ハミルトニアンは液晶エラストマーの場合と同じですが、もう一度書きますと
の場合なので、形としてはスキルミオンの場合と同じです。3次元ハミルトニアンは液晶エラストマーの場合と同じですが、もう一度書きますと
(D-21)
のようになります。ここで、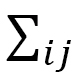 、
、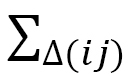 はボンドij、ボンドijを共有する4面体
はボンドij、ボンドijを共有する4面体 に関する和、
に関する和、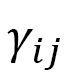 は図12(b)の4面体ijklにおける辺ij上で定義されたものです。このHはまた
は図12(b)の4面体ijklにおける辺ij上で定義されたものです。このHはまた
(D-22)
のように、4面体に関する和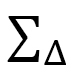 とその4面体
とその4面体 に含まれるボンドijの和
に含まれるボンドijの和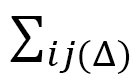 を使っても表わされます。
を使っても表わされます。
- 文献[10] V.Egorov et al.Phys. Lett. A 396 (2021) 127230 https://doi.org/10.1016/j.physleta.2021.127230
- 文献[11] H. Kawai, The Piezoelectricity of Polyvynilidene Fluoride, Jpn. J. Appl. Phys. Vol.8, p.975 (1969).
電場を加えるとなぜ縮むのかを考察します。このためには、物質内の電場と平行な直線Z軸上で、1次元的なボンドポテンシャルの線積分
(D-23)
を考えます(図24)。もちろん、液晶エラストマーの場合と同じです。
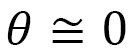 の場合:
の場合:
図24でZ軸に沿った1次元弾性エネルギー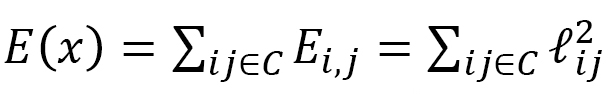 と
と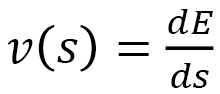 から
から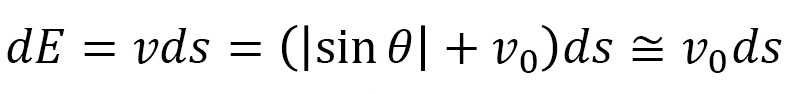 が得られるので、積分すると
が得られるので、積分すると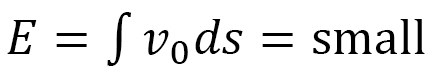 となります。ここでも、
となります。ここでも、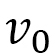 は小さな正数であることを仮定しています。左辺は
は小さな正数であることを仮定しています。左辺は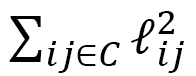 なので、 結局、
なので、 結局、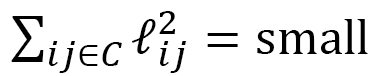 となり、これは、電場方向の分子間距離は小さくるということを表わしています。
となり、これは、電場方向の分子間距離は小さくるということを表わしています。
さらに、弾性エネルギーは張力定数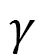 をかけたものになること、その弾性エネルギーは全体として一定になることを考えると、 Z軸上で、
をかけたものになること、その弾性エネルギーは全体として一定になることを考えると、 Z軸上で、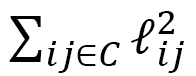 が減少するということは、この方向に関しては 有効な張力定数 が大きくなることを意味します。すなわち、電場が働いている時だけ張力定数が大きくなることも、液晶エラストマーの場合と結果は逆ですが、同じ原理です。
が減少するということは、この方向に関しては 有効な張力定数 が大きくなることを意味します。すなわち、電場が働いている時だけ張力定数が大きくなることも、液晶エラストマーの場合と結果は逆ですが、同じ原理です。
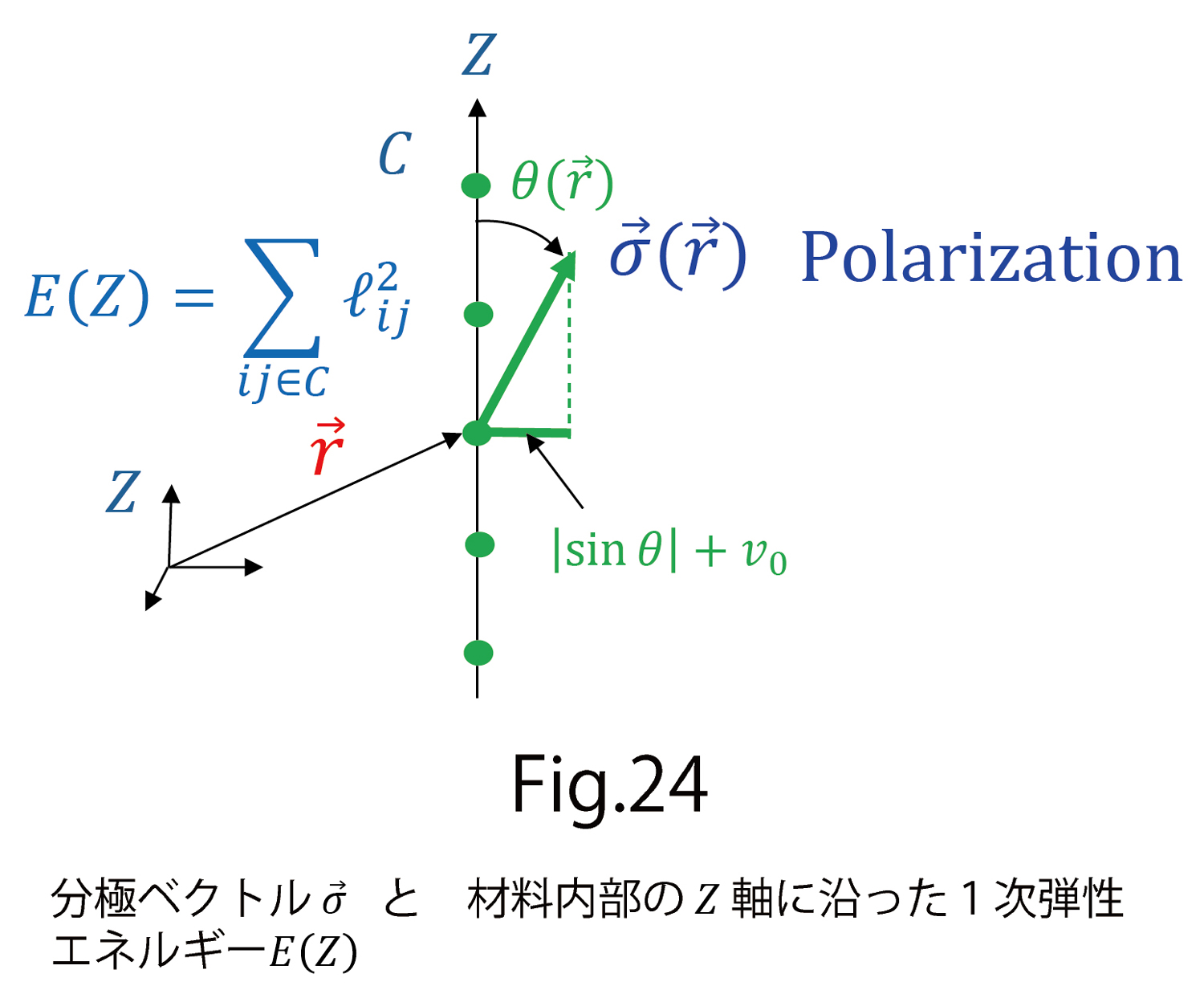
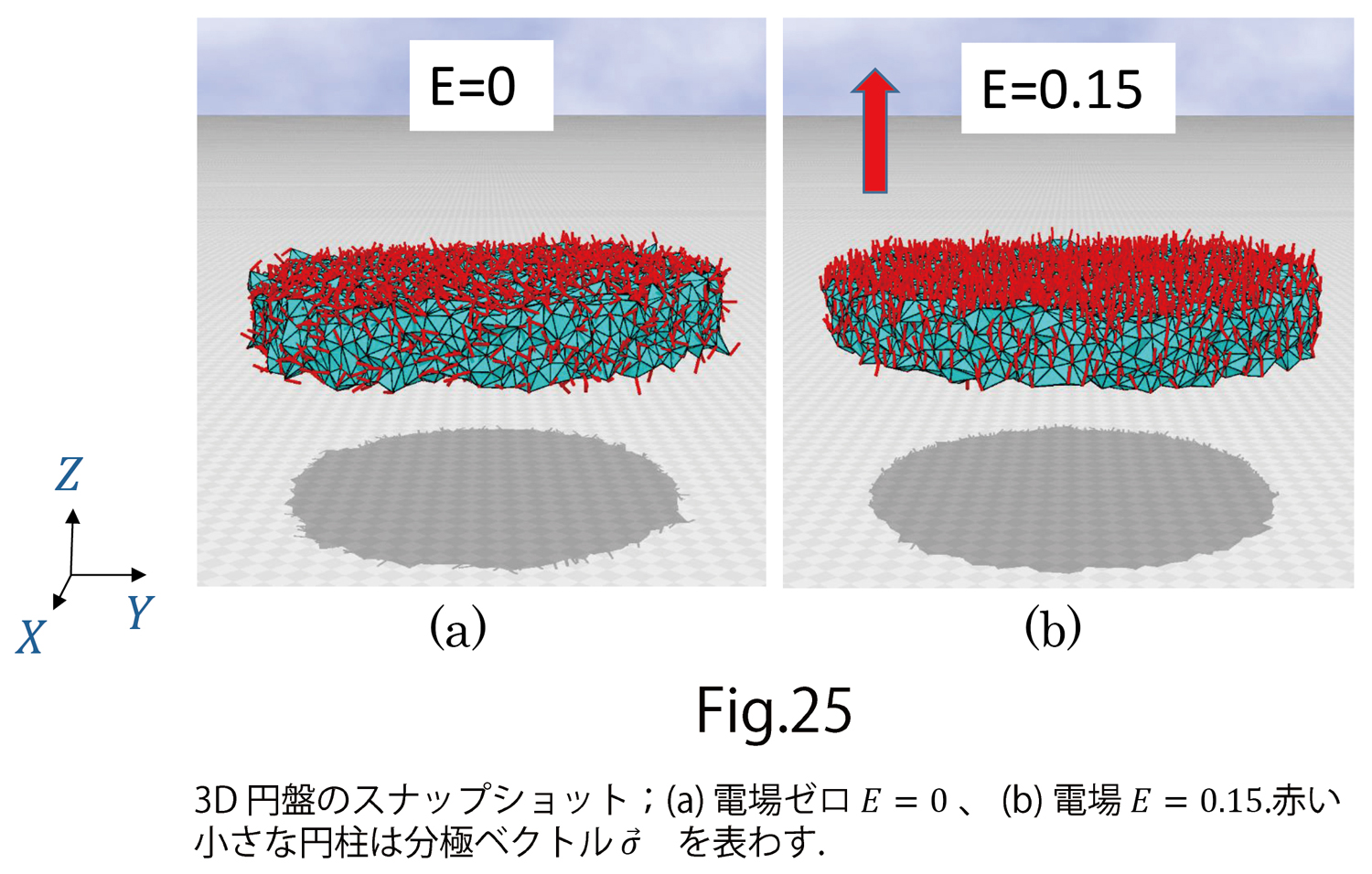
図25(a),(b)には計算結果のsnapshotを示します。図25(a)は電場ゼロ状態で、図25(b)は電場をかけた状態です。赤い細長い棒が分極ベクトル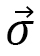 を表わしています。電場ゼロでも
を表わしています。電場ゼロでも が完全にランダムでないのは、PVDFが強誘電体であるために、電場ゼロでもある程度分極しているからです。この場合は、その分極方向は、電場をかける方向と同じくZ軸になっています。
が完全にランダムでないのは、PVDFが強誘電体であるために、電場ゼロでもある程度分極しているからです。この場合は、その分極方向は、電場をかける方向と同じくZ軸になっています。
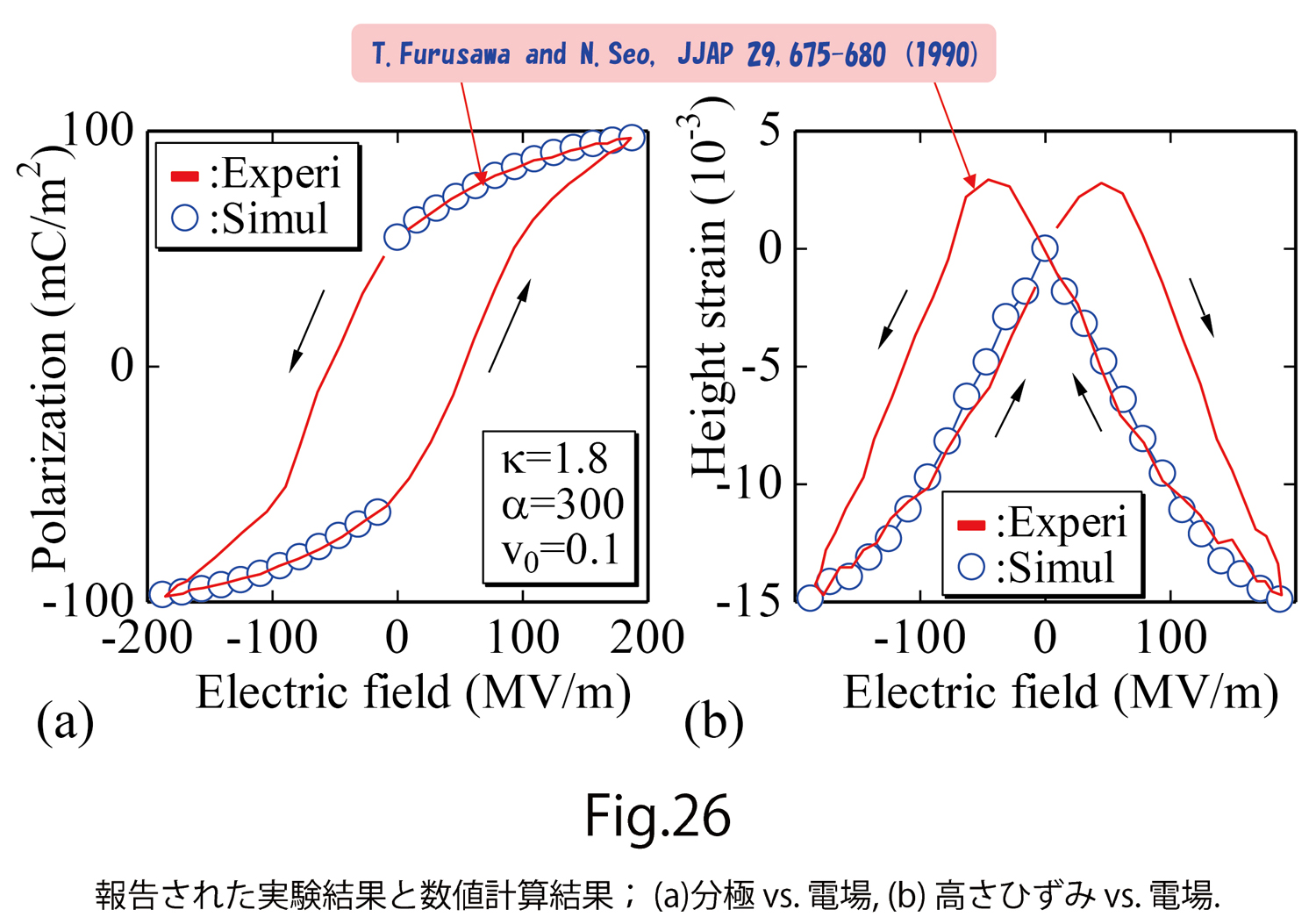
図26(a),(b)には、文献[12]に報告された実験結果と、FGモデルの計算結果を示します。図26(a)は分極 vs. 電場、図23(b)はその時のひずみ vs. 電場です。数値計算に用いた単位と実際の単位の換算の詳細はここでは省略します。ただし、ひずみは無次元なので単位の換算はないので、格子の実際のひずみそのものになっています。2つの結果は、単一のパラメータの組で計算されたもので、しかも、異方的な相互作用定数は、電場によって動的に生まれたものです。この結果も、Finsler幾何モデルの計算結果が、高い精度で実験結果と一致することを表わしています。
謝辞
仙台高専元校長 Fukumura Hiroshi先生には、再雇用期間中に研究する機会と環境を与えてくださり、大変に感謝いたします。
多くの共同研究者に感謝いたします。Matsuhisa Takashi博士、Nakayama Madoka博士、Tasaki Sohei博士らにはFinsler幾何モデルに関し有益な議論をしていただきました。
このホームページは、科研費:次世代物質探索のための離散幾何学の補助(20H04647)を受けて作成されました。
(JSPS Grant-in-Aid for Scientific Research on Innovative Areas "Discrete Geometric Analysis for Materials Design": Grant Number 20H04647)
- 文献[12] T.Furusawa and N.Seo,Electristriction as the origin of Piezoelectricity in Ferroelectric Polymers, JJAP 29,675-680 (1990).